
 x2+m過點G,求拋物線的
x2+m過點G,求拋物線的 解析式,并判斷以原點O為圓心,OG為半徑的圓與拋物線除交點G外,是否還有交點?若有,請直接寫出交點的坐標.
解析式,并判斷以原點O為圓心,OG為半徑的圓與拋物線除交點G外,是否還有交點?若有,請直接寫出交點的坐標. =8
=8 .
. )、C(0,6)
)、C(0,6)

 x+6;
x+6; ×8+6=
×8+6=
 )
) +m
+m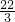
 x2-
x2-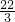
 ).
).

 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
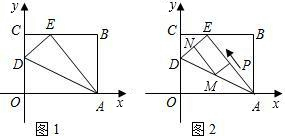
 如圖,四邊形OABC是一張放在平面直角坐標系的矩形紙片,O為原點,點A在x軸上,點C在y軸上,OA=15,OC=9,在AB上取一點M,使得△CBM沿CM翻折后,點B落在x軸上,記作N點.
如圖,四邊形OABC是一張放在平面直角坐標系的矩形紙片,O為原點,點A在x軸上,點C在y軸上,OA=15,OC=9,在AB上取一點M,使得△CBM沿CM翻折后,點B落在x軸上,記作N點.查看答案和解析>>
科目:初中數學 來源: 題型:
 OABC是一張放在平面直角坐標系中的矩形紙片,O為原點,點A在x軸上,點C在y軸上,OA=10,OC=6.
OABC是一張放在平面直角坐標系中的矩形紙片,O為原點,點A在x軸上,點C在y軸上,OA=10,OC=6.查看答案和解析>>
科目:初中數學 來源: 題型:
 的三角形相似?如果存在,請直接寫出其解析式并畫出相應的直線;如果不存在,請說明理由.
的三角形相似?如果存在,請直接寫出其解析式并畫出相應的直線;如果不存在,請說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:
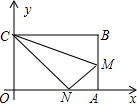
 如圖,OABC是一張放在平面直角坐標系中的矩形紙片,O為原點,點A在x軸的正半軸上,點C在y軸的正半軸上,OA=10,OC=8,在OC邊上取一點D,將紙片沿AD翻折,使點O落在BC邊上的點E處,則D點的坐標是
如圖,OABC是一張放在平面直角坐標系中的矩形紙片,O為原點,點A在x軸的正半軸上,點C在y軸的正半軸上,OA=10,OC=8,在OC邊上取一點D,將紙片沿AD翻折,使點O落在BC邊上的點E處,則D點的坐標是查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com