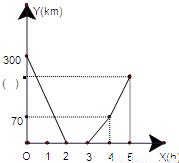
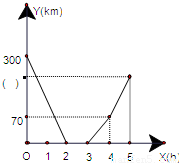
解:(1)①根據兩車間的距離y(km)與時間x(h)的函數圖象可得,兩車從出發開始到A地相遇用了2小時;
②由圖象知,從2時至3時,兩車距離為0,則兩車在A地換貨用了1小時;
③由圖象得,3時至4時,是甲車先行駛1小時走的路程,則甲車的速度為:70÷1=70km/h;
又根據兩車從出發開始到A地相遇用時2小時,則乙車的速度為:(300-70×2)÷2=80km/h;
④4時至5時,是甲乙兩車共同行駛1小時走的路程,則在圖中y軸上的小括號內應填的數字是:(70+80)×1+70=220;
故答案為:①2;②1;③70;80;④220;
(2)設4時至5時的一次函數為y=kx+b,
把(4,70)(5,220)代入得,
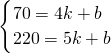
,
解得,y=150x-530,
把x=4.6代入得,y=150×4.6-530=160;
答:從兩車開始同時出發到4.6h時,甲車與乙車相距160千米.
分析:(1)①根據兩車間的距離y(km)與時間x(h)的函數圖象可得,0時至2時,是兩車從出發開始到A地相遇的用時;
②從2時至3時,兩車距離為0,則兩車在A地換貨的用時;
③根據兩車換貨后,甲車立即按原路返回北京市,而乙車又停留1小時后按原路返回石家莊市,又圖象可得出甲車的速度為70km/h;又根據兩車從出發開始到A地相遇用時2小時,可計算出乙車的速度;
④從4時至5時,為甲、乙兩車行駛的總路程,再加上70,即為小括號中應填的數字;
(2)令4時至5時的一次函數為y=kx+b,把(4,70)(5,220)代入,可得出一次函數關系式y=150x-530,把x=4.6代入,即可得出甲車與乙車相距多少千米.
點評:本題主要考查了一次函數的應用,讀懂函數圖象,弄清x軸、y軸表示的量之間的關系,是解答的關鍵.

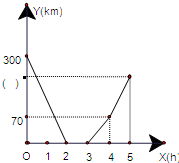 提供的信息,回答下列問題:
提供的信息,回答下列問題: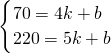 ,
,

 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案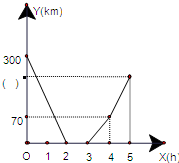 提供的信息,回答下列問題:
提供的信息,回答下列問題: