
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,DF是
,DF是![]() 的中位線,點C關于DF的對稱點為E,以DE,EF為鄰邊構造矩形DEFG,DG交BC于點H,連結CG.
的中位線,點C關于DF的對稱點為E,以DE,EF為鄰邊構造矩形DEFG,DG交BC于點H,連結CG.
![]() 求證:
求證:![]() ≌
≌![]() .
.
![]() 若
若![]() .
.
![]() 求CG的長.
求CG的長.
![]() 在
在![]() 的邊上取一點P,在矩形DEFG的邊上取一點Q,若以P,Q,C,G為頂點的四邊形是平行四邊形,求出所有滿足條件的平行四邊形的面積.
的邊上取一點P,在矩形DEFG的邊上取一點Q,若以P,Q,C,G為頂點的四邊形是平行四邊形,求出所有滿足條件的平行四邊形的面積.
![]() 在
在![]() 內取一點O,使四邊形AOHD是平行四邊形,連結OA,OB,OC,直接寫出
內取一點O,使四邊形AOHD是平行四邊形,連結OA,OB,OC,直接寫出![]() ,
,![]() ,
,![]() 的面積之比.
的面積之比.

【答案】(1)證明見解析;(2)①1;②![]() 或
或![]() 或
或![]() .(3)
.(3)![]() :3:1.
:3:1.
【解析】
![]() 根據矩形的性質、翻折不變性利用HL即可證明;
根據矩形的性質、翻折不變性利用HL即可證明;
![]() 想辦法證明
想辦法證明![]() 即可解決問題;
即可解決問題;
![]() 共三種情形畫出圖形,分別解決問題即可;
共三種情形畫出圖形,分別解決問題即可;
![]() 如圖5中,連接OD、OE、OB、
如圖5中,連接OD、OE、OB、![]() 首先證明四邊形DOHC是矩形,求出OD、OH、OE即可解決問題.
首先證明四邊形DOHC是矩形,求出OD、OH、OE即可解決問題.
![]() 如圖1中,
如圖1中,
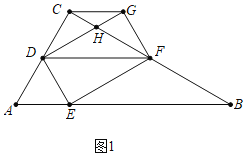
![]() 四邊形DEFG是矩形,
四邊形DEFG是矩形,
![]() ,
,![]() ,
,
由翻折不變性可知:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() 如圖1中,
如圖1中,![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 如圖2中,當點P與A重合,點Q與E重合時,四邊形PQGC是平行四邊形,此時
如圖2中,當點P與A重合,點Q與E重合時,四邊形PQGC是平行四邊形,此時![]()
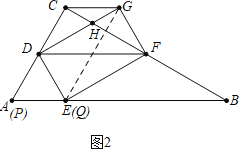
如圖3中,當四邊形QPGC是平行四邊形時,![]() .
.
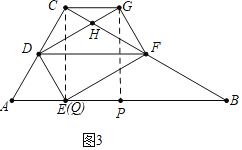
如圖4中,當四邊形PQCG是平行四邊形時,作![]() 于M,CE交DF于N.
于M,CE交DF于N.
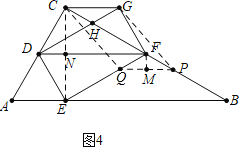
易知![]() ,
,![]() ,
,
![]()
如圖![]() 中,當四邊形PQCG是平行四邊形時,
中,當四邊形PQCG是平行四邊形時,![]() ,
,
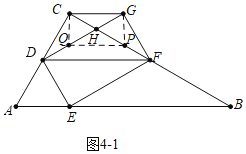
綜上所述,滿足條件的平行四邊形的面積為![]() 或
或![]() 或
或![]() .
.
![]() 如圖5中,連接OD、OE、OB、OC.
如圖5中,連接OD、OE、OB、OC.
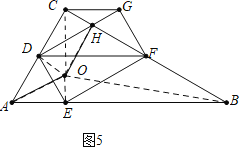
![]() 四邊形AOHD是平行四邊形,
四邊形AOHD是平行四邊形,
![]() ,
,![]() ,
,
![]() 四邊形CDOH是平行四邊形,
四邊形CDOH是平行四邊形,
![]() ,
,
![]() 四邊形CDOH是矩形,
四邊形CDOH是矩形,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() :
:![]() :
:![]() :
:![]() :
:![]() :3:1.
:3:1.


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:初中數學 來源: 題型:
【題目】某種子商店銷售“黃金一號”玉米種子,為惠民促銷,推出兩種銷售方案供采購者選擇.
方案一:每千克種子價格為4元,均不打折;
方案二:購買3千克以內(含3千克)的價格為每千克5元,若一次購買超過3千克,則超出部分的種子打七折.
(1)請分別求出方案一、方案二中購買的種子數量x(千克)與付款金額y(元)之間的函數關系式;
(2)若你去購買一定量的種子,你會怎樣選擇方案?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知∠DAB=∠DCB,AF平分∠DAB,CE平分∠DCB,∠FCE=∠CEB,試說明:AF∥CE。

解:(1)因為∠DAB=∠DCB( ),
又AF平分∠DAB,
所以_____=![]() ∠DAB( ),
∠DAB( ),
又因為CE平分∠DCB,
所以∠FCE=_____( ),
所以∠FAE=∠FCE。
因為∠FCE=∠CEB,
所以______=________
所以AF∥CE( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,正比例函數![]() 與反比例函數
與反比例函數![]() 的圖象分別交于A、C兩點,已知點B與點D關于坐標原點O成中心對稱,且點B的坐標為
的圖象分別交于A、C兩點,已知點B與點D關于坐標原點O成中心對稱,且點B的坐標為![]() 其中
其中![]() .
.
![]() 四邊形ABCD的是______
四邊形ABCD的是______![]() 填寫四邊形ABCD的形狀
填寫四邊形ABCD的形狀![]()
![]() 當點A的坐標為
當點A的坐標為![]() 時,四邊形ABCD是矩形,求m,n的值.
時,四邊形ABCD是矩形,求m,n的值.
![]() 試探究:隨著k與m的變化,四邊形ABCD能不能成為菱形?若能,請直接寫出k的值;若不能,請說明理由.
試探究:隨著k與m的變化,四邊形ABCD能不能成為菱形?若能,請直接寫出k的值;若不能,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解2016年初中畢業生畢業后的去向,某縣教育局對部分初三學生進行了抽樣調查,就初三學生的四種去向(A,讀普通高中;B,讀職業高中; C,直接進入社會就業; D,其它)進行數據統計,并繪制了兩幅不完整的統計圖(a)、(b).請根據圖中信息解答下列問題: 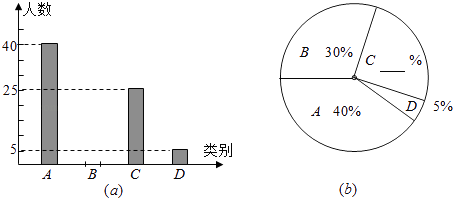
(1)該縣共調查了多少名初中畢業生?
(2)通過計算,將兩幅統計圖中不完整的部分補充完整;
(3)若該縣2016年初三畢業生共有4500人,請估計該縣今年的初三畢業生中準備讀普通高中的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是一個三角點陣,從上向下數有無數多行,其中第一行有1個點,第二行有2個點,第三行有4個點,第四行有8個點,….那么這個三角點陣中前n行的點數之和可能是( )

A. 510 B. 511 C. 512 D. 513
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE與FC會平行嗎?說明理由.
(2)AD與BC的位置關系如何?為什么?
(3)BC平分∠DBE嗎?為什么.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,折線ABCDE描述了一輛汽車在某一直線上行駛過程中,汽車離出發地的距離y(km)和行駛時間x(h)之間的函數關系,根據圖中提供的信息,給出下列說法:①汽車共行駛了120km;②汽車在行駛途中停留了0.5h;③汽車在整個行駛過程中的平均速度為![]() km/h;④汽車自出發后3h~4.5h之間行駛的速度在逐漸減小.其中正確的說法是 .(填上所有正確的序號)
km/h;④汽車自出發后3h~4.5h之間行駛的速度在逐漸減小.其中正確的說法是 .(填上所有正確的序號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一副三角板放在同一平面內,使直角頂點重合于點O
(1)如圖①,若∠AOB=155°,求∠AOD、∠BOC、∠DOC的度數.
(2)如圖①,你發現∠AOD與∠BOC的大小有何關系?∠AOB與∠DOC有何關系?直接寫出你發現的結論.
(3)如圖②,當△AOC與△BOD沒有重合部分時,(2)中你發現的結論是否還仍然成立,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com