
【題目】某班“手拉手”數學學習互助小組對矩形內兩條互相垂直的線段與矩形兩鄰邊的數量關系進行探究時,遇到以下問題,請你逐一加以解答:
(1)如圖1,正方形ABCD中,EF⊥GH,EF分別交AB,CD于點E,F,GH分別交AD,BC于點G,H,則EF GH;(填“>”“=”或“<”)
(2)如圖2,矩形ABCD中,EF⊥GH,EF分別交AB,CD于點E,F,GH分別交AD,BC于點G,H,求證:![]() =
=![]() ;
;
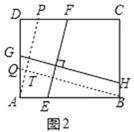
(3)如圖3,四邊形ABCD中,∠ABC=∠ADC=90°,BC=3,CD=5,AD=7.5,AM⊥DN,點M,N分別在邊BC,AB上,求![]() 的值.
的值.

【答案】(1)=;(2)見解析;(3)![]()
【解析】
(1)首先過點A作AP∥GH,交BC于P,過點B作BQ∥EF,交CD于Q,交BQ于T,然后根據正方形的性質以及△ABP≌△BCQ的判定與性質,即可得出EF=GH;
(2)首先過點A作AP∥EF,交CD于P,過點B作BQ∥GH,交AD于Q,然后根據矩形的性質以及△PDA∽△QAB的判定與性質,即可得出![]() ;
;
(3)首先過點D作平行于AB的直線,交過點A平行于BC的直線于R,交BC的延長線于S,判定平行四邊形ABSR是矩形,由(1)結論得出![]() ,然后判定△ARD∽△DSC,運用其性質和勾股定理構建方程,求解即可.
,然后判定△ARD∽△DSC,運用其性質和勾股定理構建方程,求解即可.
(1)如圖1中,過點A作AP∥GH,交BC于P,過點B作BQ∥EF,交CD于Q,交BQ于T,
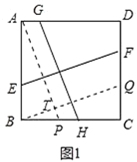
∵四邊形ABCD是正方形,
∴AB∥DC,AD∥BC,AB=BC,∠ABP=∠C=90°
∴四邊形BEFQ、四邊形PHGA都是平行四邊形,
∴AP=GH,EF=BQ.
又∵GH⊥EF,
∴AP⊥BQ,
∴∠PBT+∠ABT=90°,∠ABT+∠BAT=90°,
∴∠CBQ=∠BAT,
在△ABP和△BCQ中,
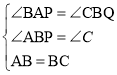 ,
,
∴△ABP≌△BCQ,
∴AP=BQ,
∴EF=GH,
故答案為:=;
(2)過點A作AP∥EF,交CD于P,過點B作BQ∥GH,交AD于Q,如圖2,
∵四邊形ABCD是矩形,
∴AB∥DC,AD∥BC.
∴四邊形AEFP、四邊形BHGQ都是平行四邊形,
∴AP=EF,GH=BQ.
又∵GH⊥EF,
∴AP⊥BQ,
∴∠QAT+∠AQT=90°,
∵四邊形ABCD是矩形,
∴∠DAB=∠D=90°,
∴∠DAP+∠DPA=90°,
∴∠AQT=∠DPA,
∴△PDA∽△QAB,
∴![]() ,
,
∴![]()
![]() ;
;
(3)過點D作平行于AB的直線,交過點A平行于BC的直線于R,交BC的延長線于S,如圖3,
則四邊形ABSR是平行四邊形.
∵∠ABC=90°,
∴平行四邊形ABSR是矩形,
∴∠R=∠S=90°,RS=AB=10,AR=BS.
∵AM⊥DN,
∴由(1)中的結論可得![]() ,
,
設SC=x,則AR=BS=3+x,
∵∠ADC=∠R=∠S=90°,
∴∠ADR+∠RAD=90°,∠ADR+∠SDC=90°,
∴∠RAD=∠CDS,
∴△ARD∽△DSC,
∴![]() =
=![]() =
=![]() ,
,
∴DR=![]() x,DS=
x,DS=![]() (x+3),
(x+3),
在Rt△ARD中,∵AD2=AR2+DR2,
∴7.52=(x+3)2+(![]() x)2,
x)2,
整理得13x2+24x﹣189=0,解得x=3或﹣![]() ,
,
∴AR=6,AB=RS=![]() ,
,
∴![]() =
=![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,是上海世博園內的一個矩形花園,花園長為100米,寬為50米,在它的四角各建有一個同樣大小的正方形觀光休息亭,四周建有與觀光休息亭等寬的觀光大道,其余部分(圖中陰影部分)種植的是不同花草.已知種植花草部分的面積為3600米2,那么矩形花園各角處的正方形觀光休息亭的邊長為多少米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校計劃一次性購買排球和籃球,每個籃球的價格比排球貴30元;購買2個排球和3個籃球共需340元.
(1)求每個排球和籃球的價格:
(2)若該校一次性購買排球和籃球共60個,總費用不超過3800元,且購買排球的個數少于39個.設排球的個數為m,總費用為y元.
①求y關于m的函數關系式,并求m可取的所有值;
②在學校按怎樣的方案購買時,費用最低?最低費用為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點F從菱形ABCD的頂點A出發,沿A→D→B以1cm/s的速度勻速運動到點B,圖2是點F運動時,△FBC的面積y(cm2)隨時間x(s)變化的關系圖象,則a的值為( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,E是AD邊的中點,BE⊥AC于點F,連接DF,下列四個結論:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四邊形CDEF=![]() S△ABF.其中正確的結論有( )個
S△ABF.其中正確的結論有( )個
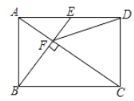
A.4B.3C.2D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
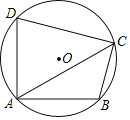
【題目】已知四邊形ABCD內接于⊙O,∠DAB=90°.
(Ⅰ)若AB=AD,求∠ACB的度數;
(Ⅱ)連接AC,若AD=8,AB=6,對角線AC平分∠DAB,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次函數![]() 與反比例函數
與反比例函數![]() 的圖象相交于A(﹣1,4),B(2,n)兩點,直線AB交x軸于點D.
的圖象相交于A(﹣1,4),B(2,n)兩點,直線AB交x軸于點D.
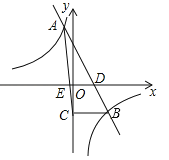
(1)求一次函數與反比例函數的表達式;
(2)過點B作BC⊥y軸,垂足為C,連接AC交x軸于點E,求△AED的面積S.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=k1x+2與反比例函數y2=![]() 的圖象交于點A(4,m)和B(﹣8,﹣2),與y軸交于點C.
的圖象交于點A(4,m)和B(﹣8,﹣2),與y軸交于點C.
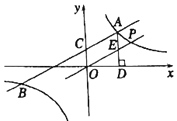
(1)k1= ,k2= ;
(2)根據函數圖象可知,當y1>y2時,x的取值范圍是 ;
(3)過點A作AD⊥x軸于點D,點P是反比例函數在第一象限的圖象上一點.設直線OP與線段AD交于點E,當S四邊形ODAC:S△ODE=3:1時,求直線OP的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與探究
如圖,拋物線![]() 經過點A(-2,0),B(4,0)兩點,與
經過點A(-2,0),B(4,0)兩點,與![]() 軸交于點C,點D是拋物線上一個動點,設點D的橫坐標為
軸交于點C,點D是拋物線上一個動點,設點D的橫坐標為![]() .連接AC,BC,DB,DC,
.連接AC,BC,DB,DC,
(1)求拋物線的函數表達式;
(2)△BCD的面積等于△AOC的面積的![]() 時,求
時,求![]() 的值;
的值;
(3)在(2)的條件下,若點M是![]() 軸上的一個動點,點N是拋物線上一動點,試判斷是否存在這樣的點M,使得以點B,D,M,N為頂點的四邊形是平行四邊形,若存在,請直接寫出點M的坐標;若不存在,請說明理由.
軸上的一個動點,點N是拋物線上一動點,試判斷是否存在這樣的點M,使得以點B,D,M,N為頂點的四邊形是平行四邊形,若存在,請直接寫出點M的坐標;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com