
【題目】已知二次函數y=x2+bx+c的圖象與直線y=x+1相交于點A(-1,m)和點B(n,5).

(1)求該二次函數的關系式;
(2)在給定的平面直角坐標系中,畫出這兩個函數的大致圖象;
(3)結合圖象直接寫出x2+bx+c>x+2時x的取值范圍.
【答案】(1)y=x2-2x-3(2)x<-1或x>4
【解析】試題分析:(1)、首先根據一次函數的解析式分別求出點A和點B的坐標,然后利用待定系數法求出二次函數的解析式;(2)、根據描點法在坐標系中畫出函數圖像,需要注意兩個函數的交點坐標;(3)、根據函數的交點將x軸分別三部分,然后根據每部分圖像的位置關系得出函數值的大小關系.
試題解析:(1)∵二次函數y=x2+bx+c的圖象與與直線y=x+1相交于點A(-1,m)和點B(n,5),∴m=-1+1=0,n+1=5,即n=4,∴點A(-1,0)和點B(4,5),∴![]() ,解得
,解得![]() ,即二次函數的解析式為y=x2-2x-3;
,即二次函數的解析式為y=x2-2x-3;
(2)這兩個函數圖象的草圖如圖所示:
 ,
,
x的取值范圍為x<-1或x>4


科目:初中數學 來源: 題型:
【題目】統計數據顯示,2018年6月中國出口鋼材694.4萬噸,同比增長2%,1﹣6月中國出口鋼材3542.6萬噸,同比減少13.2%,其中數據“694.4萬”用科學記數法表示為( )
A. 694.4×104 B. 6.944×105 C. 69.44×105 D. 6.944×106
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明一家利用國慶八天駕車到某景點旅游,小汽車出發前油箱有油35L,行駛若干小時后,途中在加油站加油若干升,油箱中余油量Q(L)與行駛時間t(h)之間的關系如圖所示,根據圖像回答下列問題:
(1)小汽車行駛______h后加油,中途加油_______L
(2)求加油前油箱余油量Q與行駛時間t的函數關系式
(3)如果小汽車在行駛過程中耗油量速度不變,加油站距景點200km,車速80km/h,要到達目的地,油箱中的油是否夠用?請說明理由

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某家電生產企業根據市場調查分析,決定調整產品生產方案,準備每周(按120個工時計算)生產空調器、彩電、冰箱共360臺,且冰箱至少生產60臺,已知生產這些家電產品每臺所需工時和每臺產值如下表:
家電名稱 | 空調 | 彩電 | 冰箱 |
工 時 |
|
|
|
產值(千元) | 4 | 3 | 2 |
問每周應生產空調器、彩電、冰箱各多少臺,才能使產值最高最高產值是多少?(以千元為單位)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 的頂點坐標為E(1,0),與
的頂點坐標為E(1,0),與![]() 軸的交點坐標為(0,1).
軸的交點坐標為(0,1).
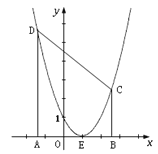

(1)求該拋物線的函數關系式.
(2)A、B是![]() 軸上兩個動點,且A、B間的距離為AB=4,A在B的左邊,過A作AD⊥
軸上兩個動點,且A、B間的距離為AB=4,A在B的左邊,過A作AD⊥![]() 軸交拋物線于D,
軸交拋物線于D,
過B作BC⊥![]() 軸交拋物線于C. 設A點的坐標為(
軸交拋物線于C. 設A點的坐標為(![]() ,0),四邊形ABCD的面積為S.
,0),四邊形ABCD的面積為S.
① 求S與![]() 之間的函數關系式.
之間的函數關系式.
② 求四邊形ABCD的最小面積,此時四邊形ABCD是什么四邊形?
③ 當四邊形ABCD面積最小時,在對角線BD上是否存在這樣的點P,使得△PAE的周長最小,若存在,請求出點P的坐標及這時△PAE的周長;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
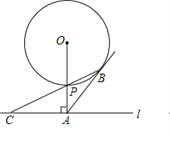
【題目】如圖,已知直線l與⊙O相離,OA⊥l于點A,OA=5,OA與⊙O相交于點P,AB與⊙O相切于點B, BP的延長線交直線l于點C.
(1)試判斷線段AB與AC的數量關系,并說明理由;
(2)若PC=![]() ,求⊙O的半徑和線段PB的長;
,求⊙O的半徑和線段PB的長;
(3)若在⊙O上存在點Q,使△QAC是以AC為底邊的等腰三角形,求⊙O的半徑r的取值范圍.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com