
【題目】某學校準備開展“陽光體育活動”,決定開設以下體育活動項目:足球、乒乓球、籃球和羽毛球,要求每位學生必須且只能選擇一項,為了解選擇各種體育活動項目的學生人數,隨機抽取了部分學生進行調查,并將獲得的數據進行整理,繪制出兩幅不完整的統計圖,請根據統計圖回答問題.


(1)這次活動一共調查了________名學生;
(2)補全條形統計圖;
(3)在扇形統計圖中,選擇籃球項目的人數所在扇形的圓心角等于________度;
(4)若該學校有1000人,請你估計該學校選擇乒乓球項目的學生人數約是________人.
【答案】(1)250;(2)補圖見解析;(3)108°;(4)160人.
【解析】
(1)直接利用足球人數÷所占百分比=總人數,即可得出答案;
(2)首先求出籃球人數進而補全條形統計圖;
(3)利用(2)中所求,得出所占百分比進而得出答案;
(4)利用乒乓球所占百分比進而估計總人數即可.
(1)由題意:80÷32%=250(人),
答:總共有250名學生;
(2)籃球人數:250-80-40-55=75(人),
如圖所示:

(3)依題意得:![]() ×360°=108°;
×360°=108°;
答:選擇籃球項目的人數所在扇形的圓心角為108°;
(4)依題意得:1000×![]() =160(人),
=160(人),
答:該學校選擇足球項目的學生人數大約為160人;


科目:初中數學 來源: 題型:
【題目】如圖,已知矩形ABCD的兩條對角線相交于點O,過點 A作AG⊥BD分別交BD、BC于點G、E.

(1)求證:BE2=EGEA;
(2)連接CG,若BE=CE,求證:∠ECG=∠EAC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將自然數按以下規律排列:

表中數2在第二行第一列,與有序數對(2,1)對應,數5與(1,3)對應,數14與(3,4)對應,根據這一規律,數2014對應的有序數對為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A、B以及直線l,AE⊥l,垂足為點E.
(1)尺規作圖:①過點B作BF⊥l,垂足為點F
②在直線l上求作一點C,使CA=CB;(要求:在圖中標明相應字母,保留作圖痕跡,不寫作法)
(2)在所作的圖中,連接CA、CB,若∠ACB=90°,∠CAE=![]() ,則∠CBF= (用含
,則∠CBF= (用含![]() 的代數式表示)
的代數式表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】王小方開了一家服裝店,專賣羽絨服,下表是去年一年各月的銷售量情況:
月份 | 一 | 二 | 三 | 四 | 五 | 六 |
銷售量/件 | 120 | 90 | 40 | 10 | 6 | 4 |
月份 | 七 | 八 | 九 | 十 | 十一 | 十二 |
銷售量/件 | 3 | 5 | 3 | 120 | 80 | 120 |
(1)計算各季度的銷售量,并用一幅合適的統計圖表示;
(2)計算各季度的銷售量在全年銷售量中所占的百分比(精確到1%),并用適當的統計圖表示;
(3)用一幅合適的統計圖表示各季度銷售量的變化情況.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“構造圖形解題”,它的應用十分廣泛,特別是有些技巧性很強的題目,如果不能發現題目中所隱含的幾何意義,而用通常的代數方法去思考,經常讓我們手足無措,難以下手,這時,如果能轉換思維,發現題目中隱含的幾何條件,通過構造適合的幾何圖形,將會得到事半功倍的效果,下面介紹兩則實例:
實例一:1876年,美國總統伽非爾德利用實例一圖證明了勾股定理:由
S四邊形ABCD=S△ABC+S△ADE+S△ABE得![]() ,化簡得:
,化簡得:![]()
實例二:歐幾里得的《幾何原本》記載,關于x的方程![]() 的圖解法是:
的圖解法是:
畫Rt△ABC,使∠ABC=90°,BC=![]() ,AC=
,AC=![]() ,再在斜邊AB上截取BD=
,再在斜邊AB上截取BD=![]() ,則AD的長就是該方程的一個正根(如實例二圖)
,則AD的長就是該方程的一個正根(如實例二圖)
請根據以上閱讀材料回答下面的問題:
(1)如圖1,請利用圖形中面積的等量關系,寫出甲圖要證明的數學公式是 ,乙圖要證明的數學公式是
(2)如圖2,若2和-8是關于x的方程x2+6x=16的兩個根,按照實例二的方式構造Rt△ABC,連接CD,求CD的長;
(3)若x,y,z都為正數,且x2+y2=z2,請用構造圖形的方法求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
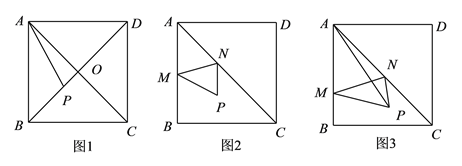
【題目】問題探究:在邊長為![]() 的正方形
的正方形![]() 中,對角線
中,對角線![]() 、
、![]() 交于點
交于點![]() .
.
探究![]() :如圖
:如圖![]() ,若點
,若點![]() 是對角線
是對角線![]() 上任意一點,則線段
上任意一點,則線段![]() 的長的取值范圍是__________;
的長的取值范圍是__________;
探究![]() :如圖
:如圖![]() ,若點
,若點![]() 是
是![]() 內任意一點,點
內任意一點,點![]() 、
、![]() 分別是
分別是![]() 邊和對角線
邊和對角線![]() 上的兩個動點,則當
上的兩個動點,則當![]() 的值在探究
的值在探究![]() 中的取值范圍內變化時,
中的取值范圍內變化時, ![]() 的周長是否存在最小值?如果存在,請求出
的周長是否存在最小值?如果存在,請求出![]() 周長的最小值,若不存在,請說明理由;
周長的最小值,若不存在,請說明理由;
問題解決:如圖![]() ,在邊長為
,在邊長為![]() 的正方形
的正方形![]() 中,點
中,點![]() 是
是![]() 內任意一點,且
內任意一點,且![]() ,點
,點![]() 、
、![]() 分別是
分別是![]() 邊和對角線
邊和對角線![]() 上的兩個動點,則當
上的兩個動點,則當![]() 的周長取到最小值時,求四邊形
的周長取到最小值時,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AD是△ABC的角平分線,CE是△ABC的高,AD與CE相交于點P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知銳角三角形ABC內接于⊙O,AD⊥BC,垂足為D.
(1)如圖1, ![]() ,BD=DC,求∠B的度數;
,BD=DC,求∠B的度數;
(2)如圖2,BE⊥AC,垂足為E,BE交AD于點F,過點B作BG∥AD交⊙O于點G,在AB邊上取一點H,使得AH=BG.求證:△AFH是等腰三角形.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com