
【題目】如圖,已知一次函數![]() 的圖像與
的圖像與![]() 軸交于點
軸交于點![]() ,一次函數
,一次函數![]() 的圖像與
的圖像與![]() 軸交于點
軸交于點![]() ,且與
,且與![]() 軸以及一次函數
軸以及一次函數![]() 的圖像分別交于點
的圖像分別交于點![]() 、
、![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.

(1)關于![]() 、
、![]() 的方程組
的方程組![]() 的解為______________.
的解為______________.
(2)關于![]() 的不等式
的不等式![]() 的解集為__________________.
的解集為__________________.
(3)求四邊形![]() 的面積;
的面積;
(4)在![]() 軸上是否存在點
軸上是否存在點![]() ,使得以點
,使得以點![]() ,
,![]() ,
,![]() 為頂點的三角形是直角三角形?若存在,求出點
為頂點的三角形是直角三角形?若存在,求出點![]() 的坐標:若不存在,請說明理由.
的坐標:若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)4;(4)點
;(3)4;(4)點![]() 坐標為
坐標為![]() 或
或![]() .
.
【解析】
(1)把D(-2,m)代入y=x-2可得D的坐標.由圖象可得結論;
(2)觀察圖象可得結論;
(3)過點D作DH⊥AB于H.根據S四邊形OADC=SΔABD-SΔOBC計算即可;
(4)分三種情況討論:①當點E為直角頂點時,過點D作DE1⊥x軸于E1,即可得出結論;
②當點C為直角頂點時,x軸上不存在點E;③當點D為直角頂點時,過點D作DE2⊥CD交x軸于點E2.設E2(t,0),利用勾股定理即可得出結論.
(1)∵D(-2,m)在y=x-2上,
∴m=-2-2=-4,
∴D(-2,-4).
由圖象可知:關于x、y的方程組![]() 的解為
的解為![]() ;
;
(2)由圖象可知:關于x的不等式x-2≥4x+b的解集為x≤-2;
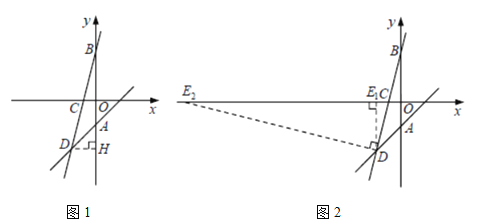
(3)如圖1,過點D作DH⊥AB于H.
由(1)知D(-2,-4),
∴DH=2.
在y=x-2中,當x=0時,y=-2,
∴A(0,-2).
把D(-2,-4)代入y=4x+b得:-4=4×(-2)+b,解得:b=4.
∴B(0,4),
∴直線BD的函數表達式為y=4x+4.
∴AB=4-(-2)=6,
∴SΔABD=![]() ABDH=
ABDH=![]() ×6×2=6.
×6×2=6.
在y=4x+4中,當y=0時,0=4x+4,解得:x=-1.
∴C(-1,0),
∴OC=1.
∵B(0,4),
∴OB=4,
∴SΔOBC=![]() OBOC=
OBOC=![]() ×4×1=2,
×4×1=2,
∴S四邊形OADC=SΔABD-SΔOBC=6-2=4.
(4)如圖2,①當點E為直角頂點時,過點D作DE
∵D(-2,-4),
∴E1(-2,0)
②當點C為直角頂點時,x軸上不存在點E.
③當點D為直角頂點時,過點D作DE2⊥CD交x軸于點E2.設E2(t,0).
∵C(-1,0),E1(-2,0),
∴CE2=-1-t,E1E2=-2-t.
∵D(-2,-4),
∴DE1=4,CE1=-1-(-2)=1.
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() .
.
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() .
.
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() .
.
∴(-1-t)2=t2+4t+20+17
解得:t=-18.
∴E2 (-18,0).
綜合上所述:點E坐標為(-2,0)或(-18,0).


 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:初中數學 來源: 題型:
【題目】在初中階段的函數學習中,我們經歷了“確定函數的表達式——利用函數圖象研究其性質——運用函數解決問題”的學習過程. 在畫函數圖象時,我們通過描點、平移、對稱的方法畫出了所學的函數圖象. 同時,我們也學習了絕對值的意義![]() ,結合上面經歷的學習過程,現在來解決下面的問題
,結合上面經歷的學習過程,現在來解決下面的問題
在函數![]() 中,自變量
中,自變量![]() 的取值范圍是全體實數,下表是
的取值范圍是全體實數,下表是![]() 與
與![]() 的幾組對應值:
的幾組對應值:
|
| 0 | 1 | 2 | 3 | ||
y | … | 0 | 1 | 2 | 3 | 2 | … |
(1)根據表格填寫:![]() _______.
_______.
(2)化簡函數解析式:
當![]() 時,
時,![]() _______;
_______;
當![]() 時,
時,![]() ______.
______.
(3)在給出的平面直角坐標系中,請用你喜歡的方法畫出這個函數的圖象并解決以下問題;
①該函數的最大值為_______.
②若![]() 為該函數圖象上不同的兩點,則
為該函數圖象上不同的兩點,則![]() ________.
________.
③根據圖象可得關于![]() 的方程
的方程![]() 的解為_______.
的解為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在邊
在邊![]() 上,
上,![]() 在線段
在線段![]() 上,
上,![]() ,
,![]() 是等邊三角形,邊
是等邊三角形,邊![]() 交邊
交邊![]() 于點
于點![]() ,邊
,邊![]() 交邊
交邊![]() 于點
于點![]() .
.
![]() 求證:
求證:![]() ;
;
![]() 當
當![]() 為何值時,以
為何值時,以![]() 為圓心,以
為圓心,以![]() 為半徑的圓與
為半徑的圓與![]() 相切?
相切?
![]() 設
設![]() ,五邊形
,五邊形![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 之間的函數解析式(要求寫出自變量
之間的函數解析式(要求寫出自變量![]() 的取值范圍);當
的取值范圍);當![]() 為何值時,
為何值時,![]() 有最大值?并求
有最大值?并求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,直線AB分別與x軸、y軸交于A、B兩點,OC平分∠AOB交AB于點C,點D為線段AB上一點,過點D作DE∥OC交y軸于點E,已知AO=m,BO=n,且m、n滿足n2﹣8n+16+|n﹣2m|=0.

(1)求A、B兩點的坐標;
(2)若點D為AB中點,求OE的長;
(3)如圖2,若點P(x,﹣2x+4)為直線AB在x軸下方的一點,點E是y軸的正半軸上一動點,以E為直角頂點作等腰直角△PEF,使點F在第一象限,且F點的橫、縱坐標始終相等,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的布袋中裝有4個只有顏色不同的球,其中1個黃球、1個藍球、2個紅球.
(1)任意摸出1個球,記下顏色后不放回,再任意摸出1個球.求兩次摸出的球恰好都是紅球的概率(要求畫樹狀圖或列表);
(2)現再將n個黃球放入布袋,攪勻后,使任意摸出1個球是黃球的概率為![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠ACD是△ABC的外角,CE平分∠ACB,交AB于E,CF平分∠ACD,EF//BC交AC、CF于M、F,若EM=3,則CE2+CF2 的值為( )

A.36B.9C.6D.18
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 是
是![]() 的中點,
的中點,![]() 是邊
是邊![]() 上一動點,連結
上一動點,連結![]() ,取
,取![]() 的中點
的中點![]() ,連結
,連結![]() .小夢根據學習函數的經驗,對
.小夢根據學習函數的經驗,對![]() 的面積與
的面積與![]() 的長度之間的關系進行了探究:
的長度之間的關系進行了探究:

(1)設![]() 的長度為
的長度為![]() ,
,![]() 的面積
的面積![]() ,通過取
,通過取![]() 邊上的不同位置的點
邊上的不同位置的點![]() ,經分析和計算,得到了
,經分析和計算,得到了![]() 與
與![]() 的幾組值,如下表:
的幾組值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 |
| 1 | 0 |
| 2 | 3 |
根據上表可知,![]() ______,
______,![]() ______.
______.
(2)在平面直角坐標系![]() 中,畫出(1)中所確定的函數的圖象.
中,畫出(1)中所確定的函數的圖象.

(3)在(1)的條件下,令![]() 的面積為
的面積為![]() .
.
①用![]() 的代數式表示
的代數式表示![]() .
.
②結合函數圖象.解決問題:當![]() 時,
時,![]() 的取值范圍為______.
的取值范圍為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 是等邊三角形,點
是等邊三角形,點![]() 在射線
在射線![]() 上,延長
上,延長![]() 至
至![]() ,使
,使![]() .
.


(1)如圖(1),當點![]() 為線段
為線段![]() 中點時,求證:
中點時,求證:![]() .
.
(2)如圖(2),當點![]() 在線段
在線段![]() 的延長線上時,
的延長線上時,![]() 還成立嗎?若成立,請給予證明;若不成立,請說明理由.
還成立嗎?若成立,請給予證明;若不成立,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com