
【題目】下列等式成立的是( )
A. (-a-b)2+(a-b)2=-4ab B. (-a-b)2+(a-b)2=a2+b2
C. (-a-b)(a-b)=(a-b)2 D. (-a-b)(a-b)=b2-a2
【答案】D
【解析】解析:∵(-a-b)2+(a-b)2=(a+b)2+(a-b)2=(a2+2ab+b2)+(a2-2ab+b2)=2a2+2b2,
∴選項A與選項B錯誤;
∵(-a-b)(a-b)=-(a+b)(a-b)=-(a2-b2)=b2-a2,∴選項C錯誤,選項D正確.
故選D.
【題型】單選題
【結束】
8
【題目】若x=1,y=![]() ,則x2+4xy+4y2的值是( )
,則x2+4xy+4y2的值是( )
A. 2 B. 4 C. 32 D. 12
科目:初中數學 來源: 題型:
【題目】在我市舉行的中學生春季田徑運動會上,參加男子跳高的15名運動員的成績如下表所示:
成績(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人數 | 1 | 2 | 4 | 3 | 3 | 2 |
這些運動員跳高成績的中位數和眾數分別是( )
A.1.70,1.65
B.1.70,1.70
C.1.65,1.70
D.3,4
查看答案和解析>>
科目:初中數學 來源: 題型:
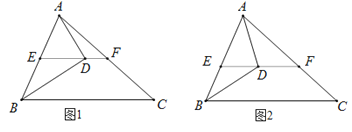
【題目】如圖,在△ABC中,點D為∠ABC的平分線BD上一點,連接AD,過點D作EF∥BC交AB于點E,交AC于點F.
(1)如圖1,若AD⊥BD于點D,∠BEF=130°,求∠BAD的度數;
(2)如圖2,若∠ABC=α,∠BDA=β,求∠FAD+∠C的度數(用含α和β的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】要調查某校學生周日的睡眠時間,下列選取調查對象中最合適的是( )
A.隨機選取該校一個班級的學生B.隨機選取該校100名男生
C.隨機選取該校一個年級的學生D.在該校各年級中隨機選取100名學生
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,CA=8,CB=6,動點P從C出發沿CA方向,以每秒1個單位長度的速度向A點勻速運動,到達A點后立即以原來速度沿AC返回;同時動點Q從點A出發沿AB以每秒1個單位長度向點B勻速運動,當Q到達B時,P、Q兩點同時停止運動.設P、Q運動的時間為t秒(t>0).
(1)當t為何值時,PQ∥CB?
(2)在點P從C向A運動的過程中,在CB上是否存在點E使△CEP與△PQA全等?若存在,求出CE的長;若不存在,請說明理由;
(3)伴隨著P、Q兩點的運動,線段PQ的垂直平分線DF交PQ于點D,交折線QB﹣BC﹣CP于點F.當DF經過點C時,求出t的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個正整數能表示為兩個正整數的平方差,則稱這個正整數為“智慧數”(如3=22-12,16=52-32,則3和16是智慧數).已知按從小到大的順序構成如下數列:3,5,7,8,9,11,12,13,15,16,17,19,20,21,23,24,25,…則第2 013個“智慧數”是______.
【答案】2 687
【解析】解析:觀察數的變化規律,可知全部“智慧數”從小到大可按每三個數分一組,從第2組開始每組的第一個數都是4的倍數,歸納可得,第n組的第一個數為4n(n≥2).因為2 013÷3=671,所以第2 013個“智慧數”是第671組中的第3個數,即為4×671+3=2 687.
點睛:找規律題需要記憶常見數列
1,2,3,4……n
1,3,5,7……2n-1
2,4,6,8……2n
2,4,8,16,32……![]()
1,4,9,16,25……![]()
2,6,12,20……n(n+1)
一般題目中的數列是利用常見數列變形而來,其中后一項比前一項多一個常數,是等差數列,列舉找規律.后一項是前一項的固定倍數,則是等比數列,列舉找規律.
【題型】填空題
【結束】
19
【題目】如圖,鄭某把一塊邊長為a m的正方形的土地租給李某種植,他對李某說:“我把你這塊地的一邊減少5 m,另一邊增加5 m,繼續租給你,你也沒有吃虧,你看如何”.李某一聽,覺得自己好像沒有吃虧,就答應了.同學們,你們覺得李某有沒有吃虧?請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com