精品日韩一区二区三区,日本不卡一二三,免费在线成人

【題目】如圖，矩形紙片ABCD中，AB=4，BC=6．將該矩形紙片剪去3個等腰直角三角形，所有剪法中剩余部分面積的最小值是（　　）

A.6
B.3
C.2.5
D.2

【答案】C
【解析】解：如圖以BC為邊作等腰直角三角形△EBC，延長BE交AD于F，得△ABF是等腰直角三角形，
作EG⊥CD于G，得△EGC是等腰直角三角形，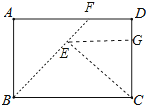

在矩形ABCD中剪去△ABF，△BCE，△ECG得到四邊形EFDG，此時剩余部分面積的最小=4×6﹣ ×4×4﹣ ×3×6﹣ ×3×3=2.5．
故選C．
以BC為邊作等腰直角三角形△EBC，延長BE交AD于F，得△ABF是等腰直角三角形，作EG⊥CD于G，得△EGC是等腰直角三角形，在矩形ABCD中剪去△ABF，△BCE，△ECG得到四邊形EFDG，此時剩余部分面積的最小本題考查幾何最值問題、等腰直角三角形性質等知識，解題的關鍵是探究出如何確定三個等腰直角三角形，屬于中考選擇題中的壓軸題．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

【題目】如圖，拋物線y= x2+ x﹣ （k＞0）與x軸交于點A、B，點A在點B的右邊，與y軸交于點C
（1）如圖1，若∠ACB=90°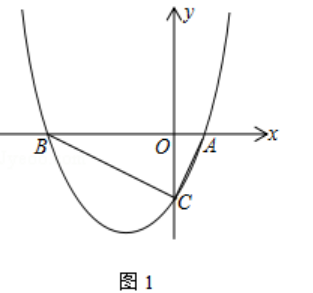

①求k的值；
②點P為x軸上方拋物線上一點，且點P到直線BC的距離為，則點P的坐標為（請直接寫出結果）
（2）如圖2，當k=2時，過原點O的任一直線y=mx（m≠0）交拋物線于點E、F（點E在點F的左邊）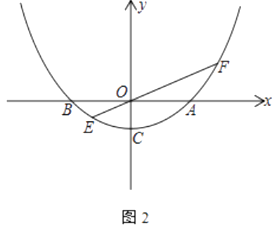

①若OF=2OE，求直線y=mx的解析式；
②求 + 的值．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】為積極響應市委政府“加快建設天藍水碧地綠的美麗長沙”的號召，我市某街道決定從備選的五種樹中選購一種進行栽種．為了更好地了解社情民意，工作人員在街道轄區范圍內隨機抽取了部分居民，進行“我最喜歡的一種樹”的調查活動（每人限選其中一種樹），并將調查結果整理后，繪制成如圖兩個不完整的統計圖：
請根據所給信息解答以下問題：
（1）這次參與調查的居民人數為：；
（2）請將條形統計圖補充完整；
（3）請計算扇形統計圖中“楓樹”所在扇形的圓心角度數；
（4）已知該街道轄區內現有居民8萬人，請你估計這8萬人中最喜歡玉蘭樹的有多少人？

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】為了提高身體素質，有些人選擇到專業的健身中心鍛煉身體，某健身中心的消費方式如下：
普通消費：35元/次；
白金卡消費：購卡280元/張，憑卡免費消費10次再送2次；
鉆石卡消費：購卡560元/張，憑卡每次消費不再收費．
以上消費卡使用年限均為一年，每位顧客只能購買一張卡，且只限本人使用．
（1）李叔叔每年去該健身中心健身6次，他應選擇哪種消費方式更合算？
（2）設一年內去該健身中心健身x次（x為正整數），所需總費用為y元，請分別寫出選擇普通消費和白金卡消費的y與x的函數關系式；
（3）王阿姨每年去該健身中心健身至少18次，請通過計算幫助王阿姨選擇最合算的消費方式．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】甲、乙兩家草莓采摘園的草莓品質相同，銷售價格也相同．“五一期間”，兩家均推出了優惠方案，甲采摘園的優惠方案是：游客進園需購買50元的門票，采摘的草莓六折優惠；乙采摘園的優惠方案是：游客進園不需購買門票，采摘園的草莓超過一定數量后，超過部分打折優惠．優惠期間，設某游客的草莓采摘量為x（千克），在甲采摘園所需總費用為y1（元），在乙采摘園所需總費用為y2（元），圖中折線OAB表示y2與x之間的函數關系．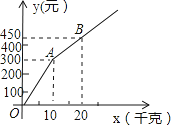

（1）甲、乙兩采摘園優惠前的草莓銷售價格是每千克元；
（2）求y1、y2與x的函數表達式；
（3）在圖中畫出y1與x的函數圖象，并寫出選擇甲采摘園所需總費用較少時，草莓采摘量x的范圍．