
【題目】閱讀與應用:
閱讀1:a、b為實數,且a>0,b>0,因為![]() ,所以
,所以![]() ,從而
,從而![]() (當a=b時取等號).
(當a=b時取等號).
閱讀2:函數![]() (常數m>0,x>0),由閱讀1結論可知:
(常數m>0,x>0),由閱讀1結論可知: ![]()
![]() ,所以當
,所以當![]() 即
即![]() 時,函數
時,函數![]() 的最小值為
的最小值為![]() .
.
閱讀理解上述內容,解答下列問題:
問題1:已知一個矩形的面積為4,其中一邊長為x,則另一邊長為![]() ,周長為
,周長為![]() ,求當x=__________時,周長的最小值為__________.
,求當x=__________時,周長的最小值為__________.
問題2:已知函數y1=x+1(x>-1)與函數y2=x2+2x+17(x>-1),當x=__________時, ![]() 的最小值為__________.
的最小值為__________.
問題3:某民辦學習每天的支出總費用包含以下三個部分:一是教職工工資6400元;二是學生生活費每人10元;三是其他費用.其中,其他費用與學生人數的平方成正比,比例系數為0.01.當學校學生人數為多少時,該校每天生均投入最低?最低費用是多少元?(生均投入=支出總費用÷學生人數)
【答案】問題1: 2 8 問題2: 3 8 問題3:設學校學生人數為x人,生均投入為y元,依題意得: ![]() ,因為x>0,所以
,因為x>0,所以![]() ,當
,當![]() 即x=800時,y取最小值26.答:當學校學生人數為800人時,該校每天生均投入最低,最低費用是26元.
即x=800時,y取最小值26.答:當學校學生人數為800人時,該校每天生均投入最低,最低費用是26元.
【解析】試題
問題1:當![]() 時,周長有最小值,求x的值和周長最小值;
時,周長有最小值,求x的值和周長最小值;
問題2:變形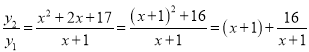 ,由當x+1=
,由當x+1=![]() 時,
時, ![]() 的最小值,求出x值和
的最小值,求出x值和![]() 的最小值;
的最小值;
問題3:設學校學生人數為x人,生均投入為y元,根據生均投入=支出總費用÷學生人數,列出關系式,根據前兩題解法,從而求解.
試題解析:
問題1:∵當![]() ( x>0)時,周長有最小值,
( x>0)時,周長有最小值,
∴x=2,
∴當x=2時,![]() 有最小值為
有最小值為![]() =4.即當x=2時,周長的最小值為2×4=8;
=4.即當x=2時,周長的最小值為2×4=8;
問題2:∵y1=x+1(x>-1)與函數y2=x2+2x+17(x>-1),
∴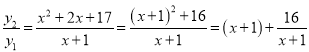 ,
,
∵當x+1=![]() (x>-1)時,
(x>-1)時, ![]() 的最小值,
的最小值,
∴x=3,
∴x=3時, ![]() 有最小值為4+4=8,即當x=3時,
有最小值為4+4=8,即當x=3時, ![]() 的最小值為8;
的最小值為8;
問題3:設學校學生人數為x人,則生均投入y元,依題意得
![]() ,因為x>0,所以
,因為x>0,所以![]() ,當
,當![]() 即x=800時,y取最小值26.
即x=800時,y取最小值26.
答:當學校學生人數為800


科目:初中數學 來源: 題型:
【題目】已知,如圖:在平面直角坐標系中,點D是直線y=﹣x上一點,過O、D兩點的圓⊙O1分別交x軸、y軸于點A和B.
(1)當A(﹣12,0),B(0,﹣5)時,求O1的坐標;

(2)在(1)的條件下,過點A作⊙O1的切線與BD的延長線相交于點C,求點C的坐標;

(3)若點D的橫坐標為![]() ,點I為△ABO的內心,IE⊥AB于E,當過O、D兩點的⊙O1的大小發生變化時,其結論:AE﹣BE的值是否發生變化?若不變,請求出其值;若變化,請求出變化范圍.
,點I為△ABO的內心,IE⊥AB于E,當過O、D兩點的⊙O1的大小發生變化時,其結論:AE﹣BE的值是否發生變化?若不變,請求出其值;若變化,請求出變化范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
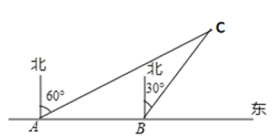
【題目】為了維護國家主權和海洋權力,海監部門對我國領海實行常態化巡航管理,如圖,正在執行巡航任務的海監船以每小時30海里的速度向正東方航行,在![]() 處測得燈塔
處測得燈塔![]() 在北偏東60°方向上, 繼續航行
在北偏東60°方向上, 繼續航行![]() 后到達
后到達![]() 處, 此時測得燈塔
處, 此時測得燈塔![]() 在北偏東30°方向上.
在北偏東30°方向上.
(1) 求![]() 的度數;
的度數;
(2)已知在燈塔![]() 的周圍15海里內有暗礁,問海監船繼續向正東方向航行是否安全?
的周圍15海里內有暗礁,問海監船繼續向正東方向航行是否安全?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校為了調查學生對教學的滿意度,隨機抽取了部分學生作問卷調查:用“![]() ”表示“很滿意”,“
”表示“很滿意”,“![]() ”表示“滿意”,“
”表示“滿意”,“![]() ”表示“比較滿意”,“
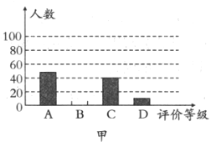
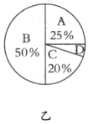
”表示“比較滿意”,“![]() ”表示“不滿意”,下圖是工作人員根據問卷調查統計資料繪制的兩幅不完整的統計圖,請你根據統計圖提供的信息解答以下問題:
”表示“不滿意”,下圖是工作人員根據問卷調查統計資料繪制的兩幅不完整的統計圖,請你根據統計圖提供的信息解答以下問題:
(1)本次問卷調查,共調查了多少名學生?
(2)將圖甲中“![]() ”部分的圖形補充完整;
”部分的圖形補充完整;
(3)求出圖乙中扇形![]() 的圓心角的度數.
的圓心角的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
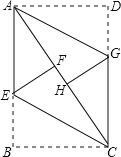
【題目】如圖,ABCD是矩形紙片,翻折∠B、∠D,使BC、AD恰好落在AC上.設F、H分別是B、D落在AC上的兩點,E、G分別是折痕CE、AG與AB、CD的交點.
(1)求證:四邊形AECG是平行四邊形:
(2)若AB=8cm,BC=6cm,求線段EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, 在8×8的正方形網格中,△ABC的頂點在邊長為1的小正方形的頂點上
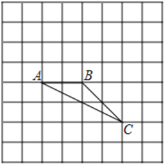
(1) 填空∠ABC=___________
(2) 若點A在網格所在的坐標平面內的坐標為(1,-2),請建立平面直角坐標系,D是平面直角坐標系中一點,并作出以A、B、C、D四個點為頂點的平行四邊形,直接寫出滿足條件的D點的坐標
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】光華農機租賃公司共有50臺聯合收割機,其中甲型20臺,乙型30臺,先將這50臺聯合收割機派往A、B兩地區收割小麥,其中30臺派往A地區,20臺派往B地區.兩地區與該農機租賃公司商定的每天的租賃價格見表:
每臺甲型收割機的租金 | 每臺乙型收割機的租金 | |
A地區 | 1800 | 1600 |
B地區 | 1600 | 1200 |
(1)設派往A地區x臺乙型聯合收割機,租賃公司這50臺聯合收割機一天獲得的租金為y(元),求y與x間的函數關系式,并寫出x的取值范圍;
(2)若使農機租賃公司這50臺聯合收割機一天獲得的租金總額不低于79 600元,說明有多少種分配方案,并將各種方案設計出來;
(3)如果要使這50臺聯合收割機每天獲得的租金最高,請你為光華農機租賃公司提一條合理化建議.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是正方形,點E、F分別在AD、CD上,AF、BE相交于點G,且AF=BE,則下列結論不正確的是:( )
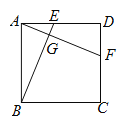
A.AF⊥BEB.BG=GFC.AE=DFD.∠EBC=∠AFD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按要求作圖
在下面的網格中,已知△ABC的頂點分別落在網格的格點,點A′、C′分別是點A、C兩點繞某一點O旋轉同樣的角度后的對應點.
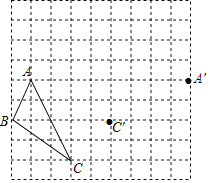
(1)請在下圖中作出旋轉中心O的位置;
(2)點A′是點A繞點O旋轉 度形成的;
(3)畫出△ABC繞點O旋轉同樣的角度后的△A′B'C’.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com