解:(1)由題意可得:
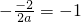
∴a=-1,
則y=-x
2-2x+3
∴y=-(x+1)
2+4,
∴頂點D的坐標是(-1,4);
(2)∵P是y軸上一點,
∴設點P的坐標為(0,y)
又∵∠COB=90°,∠PCB≠90°
∴⒈當∠CPB=90°=∠COB 則點P的坐標為(0,0)此時△CPB∽△COB,
⒉當∠CBP=90°=∠COB時,則△CBP∽△COB,
∴∠OCB=∠PBO,
∴△COB∽△BOP,
∴
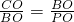
--------------(7分)
又∵y=-x
2-2x+3,
∴點C坐標是(0,3)、點B的坐標是(1,0)
∴
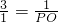
,
∴
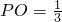
∴點P的坐標是(

)-------------(9分)
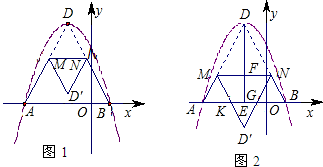
(3)設DM=x,作DE⊥AB,垂足為E,交MN于點F,
∵點D(-1,4)
∴
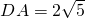
①當
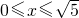
時(圖1),
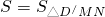
由折疊可知,

∵MN∥AB,
∴△DMN∽△DAB
∴
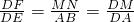
即
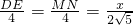
,
∴
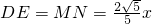
∴

------------------(10分)
∴當
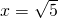
時,S
max=2;--------------------(11分)
②當
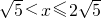
時,如圖2,則S=S
梯形MNGK由折疊可知:∠DMN=∠D′MN,
又∵MN∥AB
∴∠DMN=∠DAB∠NMK=∠MKA
∴∠MAK=∠MKA
∴MK=MA=
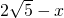
∴
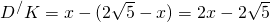
由△D′KG∽△D′MN得,
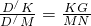
∴
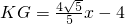
又∵
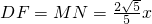
∴
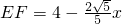
∴
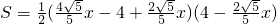
=
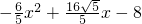
------------(12分)
∴
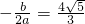
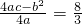
又∵
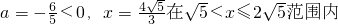
∴當
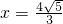
時
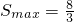
,------------------------------------(13分)
綜合上面分析可知:
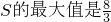
.------------------------------(14分)
分析:(1)根據其對稱軸為x=-1,求得a的值,代入函數關系式即可求得其頂點坐標;
(2)設出p點的坐標,利用兩三角形相似得到有關的方程,解得后即可求得p點的坐標;
(3)設DM=x,作DE⊥AB,垂足為E,交MN于點F,求得線段DA的長,分當
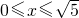
時和當
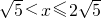
時兩種情況求得重疊部分的最大面積即可.
點評:本題主要考查了二次函數的性質,三角形相似的性質,梯形的面積公式,用待定系數法求二次函數的解析式等知識點,能綜合運用這些知識解題是解決本題的關鍵.難點是(3)小題的求法,巧妙地運用了分類討論思想.

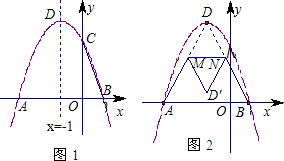 ,把△DMN沿MN折疊得△D′MN,設△D′MN與△ABD的重疊部分的面積為S,請探究:S的最大值.
,把△DMN沿MN折疊得△D′MN,設△D′MN與△ABD的重疊部分的面積為S,請探究:S的最大值. 解:(1)由題意可得:
解:(1)由題意可得: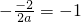
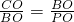 --------------(7分)
--------------(7分)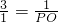 ,
,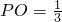
 )-------------(9分)
)-------------(9分)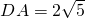
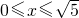 時(圖1),
時(圖1),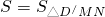

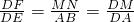
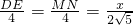 ,
,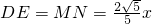
 ------------------(10分)
------------------(10分)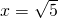 時,Smax=2;--------------------(11分)
時,Smax=2;--------------------(11分)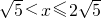 時,如圖2,則S=S梯形MNGK
時,如圖2,則S=S梯形MNGK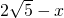
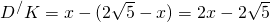
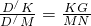
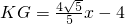
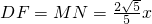
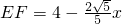
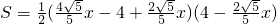 =
=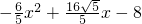 ------------(12分)
------------(12分)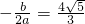
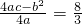
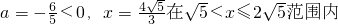
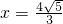 時
時 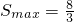 ,------------------------------------(13分)
,------------------------------------(13分)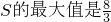 .------------------------------(14分)
.------------------------------(14分)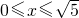 時和當
時和當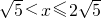 時兩種情況求得重疊部分的最大面積即可.
時兩種情況求得重疊部分的最大面積即可.


 如圖,在平面直角坐標中,已知直線y=kx+b與直線y=
如圖,在平面直角坐標中,已知直線y=kx+b與直線y= 如圖,在平面直角坐標xOy中,已知點A(-5,0),P是反比例函數y=
如圖,在平面直角坐標xOy中,已知點A(-5,0),P是反比例函數y=