已知四個互不相等的實數x1,x2,x3,x4,其中x1<x2,x3<x4.
(1)請列舉x1,x2,x3,x4從小到大排列的所有可能情況;
(2)已知a為實數,函數y=x2-4x+a與x軸交于(x1,0),(x2,0)兩點,函數y=x2+ax-4與x軸交于(x3,0),(x4,0)兩點.若這四個交點從左到右依次標為A,B,C,D,且AB=BC=CD,求a的值.
【答案】
分析:(1)可以這樣理解:x
1或x
3最小,x
2或x
4最大,以此排列即可;
(2)將利用二次函數兩點間的距離公式解答.
解答:解:(1)x
1<x
2<x
3<x
4,x
1<x
3<x
2<x
4,x
1<x
3<x
4<x
2,x
3<x
4<x
1<x
2,x
3<x
1<x
4<x
2,x
3<x
1<x
2<x
4;
(2)上述6種情況中第3,6種情況不可能出現.否則,兩個函數的對稱軸相同,則a=-4,從而x
1=x
3,x
2=x
4,這與題意不符,
在其他4種情況中,都有|x
2-x
1|=|x
4-x
3|,因此有
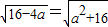
,即a=0或-4(舍去),經檢驗a=0滿足題意.
點評:解答此題要明確兩點間的距離公式:|x
2-x
1|=
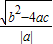
.
