
【題目】某大眾汽車經銷商在銷售某款汽車時,以高出進價20%標價.已知按標價的九折銷售這款汽車9輛與將標價直降0.2萬元銷售4輛獲利相同.
(1)求該款汽車的進價和標價分別是多少萬元?
(2)若該款汽車的進價不變,按(1)中所求的標價出售,該店平均每月可售出這款汽車20輛;若每輛汽車每降價0.1萬元,則每月可多售出2輛.求該款汽車降價多少萬元出售每月獲利最大?最大利潤是多少?
【答案】
(1)
解:設進價為x萬元,則標價是1.2x萬元,由題意得:
1.2x×0.9×9﹣9x=(1.2x﹣0.2)×4﹣4x,
解得:x=10,
1.2×10=12(萬元),
答:進價為10萬元,標價為12萬元
(2)
解:設該款汽車降價a萬元,利潤為w萬元,由題意得:
w=(20+ ![]() ×2)(12﹣10﹣a),
×2)(12﹣10﹣a),
=﹣20(a﹣ ![]() )2+45,
)2+45,
∵﹣20<0,
∴當a= ![]() 時,w最大=45,
時,w最大=45,
答:該款汽車降價0.5萬元出售每月獲利最大,最大利潤是45萬元
【解析】(1)設進價為x萬元,則標價是1.2x萬元,根據關鍵語句:按標價的九折銷售這款汽車9輛的利潤是1.2x×0.9×9﹣9x,將標價直降0.2萬元銷售4輛獲利是(1.2x﹣0.2)×4﹣4x,根據利潤相等可得方程1.2x×0.9×9﹣9x=(1.2x﹣0.2)×4﹣4x,再解方程即可得到進價,進而得到標價;(2)設該款汽車降價a萬元,利潤為w萬元,利用銷售量×每輛汽車的利潤=總利潤列出函數關系式,再利用配方法求最值即可.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,E為AB邊上一點,過點D作DF⊥DE,與BC延長線交于點F.連接EF,與CD邊交于點G,與對角線BD交于點H.
(1)若BF=BD=![]() ,求BE的長;
,求BE的長;
(2)若∠ADE=2∠BFE,求證:FH=HE+HD.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某汽車銷售公司經銷某品牌A、B兩款汽車,已知A款汽車每輛進價為![]() 萬元,B款汽車每輛進價為6萬元.
萬元,B款汽車每輛進價為6萬元.
![]() 公司預計用不多于135萬元且不少于129萬元的資金購進這兩款汽車共20輛,有幾種進貨方案,它們分別是什么?
公司預計用不多于135萬元且不少于129萬元的資金購進這兩款汽車共20輛,有幾種進貨方案,它們分別是什么?
![]() 如果A款汽車每輛售價為9萬元,B款汽車每輛售價為8萬元,為打開B款汽車的銷路,公司決定每售出一輛B款汽車,返還顧客現金a萬元,要使
如果A款汽車每輛售價為9萬元,B款汽車每輛售價為8萬元,為打開B款汽車的銷路,公司決定每售出一輛B款汽車,返還顧客現金a萬元,要使![]() 中所有的方案獲利相同,a值應是多少,此種方案是什么?(提示:可設購進B款汽車x輛)
中所有的方案獲利相同,a值應是多少,此種方案是什么?(提示:可設購進B款汽車x輛)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線l∥AB,l與AB之間的距離為2.C、D是直線l上兩個動點(點C在D點的左側),且AB=CD=5.連接AC、BC、BD,將△ABC沿BC折疊得到△A′BC.下列說法:①四邊形ABCD的面積始終為10;②當A′與D重合時,四邊形ABDC是菱形;③當A′與D不重合時,連接A′、D,則∠CA′D+∠BCA′=180°;④若以A′、C、B、D為頂點的四邊形為矩形,則此矩形相鄰兩邊之和為3![]() 或7.其中正確的是( )
或7.其中正確的是( )

A. ①②④ B. ①③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,距小明家樓下D點20米的B處有一根廢棄的電線桿AB,經測得此電線桿與水平線DB所成銳角為60°,在小明家樓頂C處測得電線桿頂端A的俯角為30°,底部點B的俯角為45°(點A、B、D、C在同一平面內).已知在以點B為圓心,10米長為半徑的圓形區域外是一休閑廣場,有關部門想把此電線桿水平放倒,且B點不動,為安全起見,他們想知道這根電線桿放倒后,頂端A能否落在休閑廣場內?請通過計算回答.
(結果精確到0.1米,參考數據: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)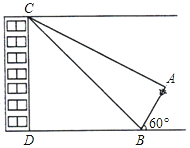
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】蝸牛從某點![]() 開始沿一東西方向直線爬行,規定向東爬行的路程記為正數,向西爬行的路程記為負數.爬過的各段路程依次為(單位:厘米):
開始沿一東西方向直線爬行,規定向東爬行的路程記為正數,向西爬行的路程記為負數.爬過的各段路程依次為(單位:厘米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 通過計算說明蝸牛是否回到起點
通過計算說明蝸牛是否回到起點![]() .
.
![]() 蝸牛離開出發點
蝸牛離開出發點![]() 最遠時是多少厘米?
最遠時是多少厘米?
![]() 在爬行過程中,如果每爬
在爬行過程中,如果每爬![]() 厘米獎勵
厘米獎勵![]() 粒芝麻,則蝸牛一共得到多少粒芝麻?
粒芝麻,則蝸牛一共得到多少粒芝麻?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在△AOB與△COD中,OA=OB,OC=OD,∠AOB=∠COD=90°.
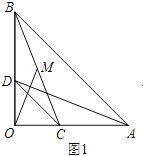
(1)如圖1,點C、D分別在邊OA、OB上,連結AD、BC,點M為線段BC的中點,連結OM,則請你判斷線段AD與OM之間的數量關系,并加以證明.
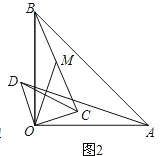
(2)如圖2,將圖1中的△COD繞點O逆時針旋轉,旋轉角為α(0°<α<90°).連結AD、BC,點M為線段BC的中點,連結OM.請你判斷(1)中的結論是否仍然成立.若成立,請證明;若不成立,請說明理由;
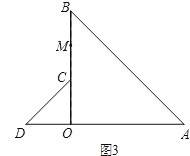
(3)如圖3,將圖1中的△COD繞點O逆時針旋轉到使△COD的一邊OD恰好與△AOB的邊OA在同一條直線上時,點C落在OB上,點M為線段BC的中點.請你判斷(1)中線段AD與OM之間的數量關系是否發生變化,寫出你的猜想,并加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法:(1)相反數是本身的數是正數;(2)兩數相減,差小于被減數;(3)絕對值等于它相反數的數是負數;(4)倒數是它本身的數是1;(5)若![]() ,則a=b;(6)沒有最大的正數,但有最大的負整數.其中正確的個數( )
,則a=b;(6)沒有最大的正數,但有最大的負整數.其中正確的個數( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
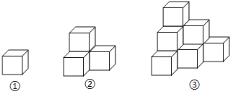
【題目】根據三視圖求幾何體的表面積.
下列各圖是棱長為![]() 的小正方體擺成的,如圖①中,共有
的小正方體擺成的,如圖①中,共有![]() 個小正方體,從正面看有
個小正方體,從正面看有![]() 個正方形,表面積為
個正方形,表面積為![]() ;如圖②中,共有
;如圖②中,共有![]() 個小正方體,從正面看有
個小正方體,從正面看有![]() 個正方形,表面積為
個正方形,表面積為![]() ;如圖③,共有
;如圖③,共有![]() 個小正方體,從正面看有
個小正方體,從正面看有![]() 個正方形,表面積為
個正方形,表面積為![]() ;…
;…
![]() 第
第![]() 個圖中,共有多少個小正方體?從正面看有多少個正方形?表面積是多少?
個圖中,共有多少個小正方體?從正面看有多少個正方形?表面積是多少?
![]() 第
第![]() 個圖形中,從正面看有多少個正方形?表面積是多少?
個圖形中,從正面看有多少個正方形?表面積是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com