
【題目】如圖,在矩形ABCD中,AB=8,AD=6,點M為對角線AC上的一個動點(不與端點A,C重合),過點M作ME⊥AD,MF⊥DC,垂足分別為E,F,則四邊形EMFD面積的最大值為( )
A.6
B.12
C.18
D.24
【答案】B
【解析】解:∵四邊形ABCD是矩形,
∴∠D=90°,
∵ME⊥AD,MF⊥DC,
∴∠DEM=90°,∠DFM=90°,
∴四邊形EDFM是矩形;
∴DF=EM,DE=FM,FM∥AD,ME∥CD,
∴△AEM∽△ADC,
∴ ![]() =
= ![]() ,
,
設DF=EM=x,DE=FM=y,
∴ ![]() =
= ![]() ,
,
y=﹣ ![]() x+6,
x+6,
四邊形EMFD面積=xy=x(﹣ ![]() x+6)=﹣
x+6)=﹣ ![]() (x﹣4)2+12,
(x﹣4)2+12,
故x=4時,四邊形EMFD面積的最大值為12.
所以答案是:B.
【考點精析】本題主要考查了二次函數的最值和相似三角形的判定與性質的相關知識點,需要掌握如果自變量的取值范圍是全體實數,那么函數在頂點處取得最大值(或最小值),即當x=-b/2a時,y最值=(4ac-b2)/4a;相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】從數﹣2,﹣ ![]() ,0,4中任取一個數記為m,再從余下的三個數中,任取一個數記為n,若k=mn,則正比例函數y=kx的圖象經過第三、第一象限的概率是 .
,0,4中任取一個數記為m,再從余下的三個數中,任取一個數記為n,若k=mn,則正比例函數y=kx的圖象經過第三、第一象限的概率是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,點P在∠AOB內,點M、N分別是點P關于AO、BO所在直線的對稱點.
(1)若△PEF的周長為20,求MN的長.
(2)若∠O=50°,求∠EPF的度數.
(3)請直接寫出∠EPF與∠O的數量關系是_____________________________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,則CE2+CF2等于( )
A.75
B.100
C.120
D.125
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,則∠A、∠C、∠E、∠F滿足的數量關系是( )

A. ∠A=∠C+∠E+∠F B. ∠A+∠E﹣∠C﹣∠F=180°
C. ∠A﹣∠E+∠C+∠F=90° D. ∠A+∠E+∠C+∠F=360°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:在平面直角坐標系中,點A、B為函數L圖象上的任意兩點,點A坐標為(x1 , y1),點B坐標為(x2 , y2),把式子 ![]() 稱為函數L從x1到x2的平均變化率;對于函數K:y=2x2﹣3x+1圖象上有兩點A(x1 , y1)和B(x2 , y2),當x1=1,x2﹣x1=
稱為函數L從x1到x2的平均變化率;對于函數K:y=2x2﹣3x+1圖象上有兩點A(x1 , y1)和B(x2 , y2),當x1=1,x2﹣x1= ![]() 時,函數K從x1到x2的平均變化率是;當x1=1,x2﹣x1=
時,函數K從x1到x2的平均變化率是;當x1=1,x2﹣x1= ![]() (n為正整數)時,函數K從x1到x2的平均變化率是 .
(n為正整數)時,函數K從x1到x2的平均變化率是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,![]() 為坐標原點,四邊形
為坐標原點,四邊形![]() 是矩形,點
是矩形,點![]() 的坐標分別為
的坐標分別為![]() ,點
,點![]() 以
以![]() 的速度從
的速度從![]() 出發向終點
出發向終點![]() 運動,點
運動,點![]() 以
以![]() 的速度從
的速度從![]() 出發向終點
出發向終點![]() 運動,當
運動,當![]() 是以
是以![]() 為一腰的等腰三角形時,點
為一腰的等腰三角形時,點![]() 的坐標為____.
的坐標為____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠B=∠C=45°,點D在BC邊上,點E在AC邊上,且∠ADE=∠AED,連結DE.
(1)當∠BAD=60°,求∠CDE的度數;
(2)當點D在BC(點B、C除外)邊上運動時,試寫出∠BAD與∠CDE的數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
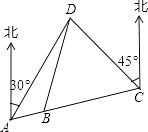
【題目】某市開展一項自行車旅游活動,線路需經A,B,C,D四地,如圖,其中A,B,C三地在同一直線上,D地在A地北偏東30°方向,在C地北偏西45°方向,C地在A地北偏東75°方向.且BC=CD=20km,問沿上述線路從A地到D地的路程大約是多少?(最后結果保留整數,參考數據:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, ![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com