
【題目】如圖,PB與⊙O相切于點B,過點B作OP的垂線BA,垂足為C,交⊙O于點A,連結PA,AO,AO的延長線交⊙O于點E,與PB的延長線交于點D.
(1)求證:PA是⊙O的切線;
(2)若tan∠BAD=![]() ,且OC=4,求BD的長.
,且OC=4,求BD的長.
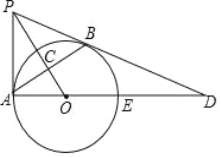
【答案】(1)證明見解析;(2)![]()
【解析】試題分析:(1)連接OB,由SSS證明△PAO≌△PBO,得出∠PAO=∠PBO=90°即可;
(2)連接BE,證明△PAC∽△AOC,證出OC是△ABE的中位線,由三角形中位線定理得出BE=2OC,由△DBE∽△DPO可求出.
試題解析:(1)連結OB,則OA=OB.如圖1,
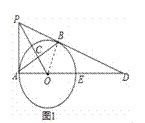
∵OP⊥AB,
∴AC=BC,∴OP是AB的垂直平分線,∴PA=PB.
在△PAO和△PBO中,
∵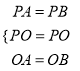 ,
,
∴△PAO≌△PBO(SSS),
∴∠PBO=∠PAO.∵PB為⊙O的切線,B為切點,∴∠PBO=90°,
∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切線;
(2)連結BE.如圖2,
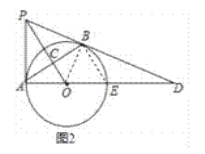
∵在Rt△AOC中,tan∠BAD=tan∠CAO=![]() ,且OC=4,
,且OC=4,
∴AC=6,則BC=6.在Rt△APO中,∵AC⊥OP,
∴△PAC∽△AOC,∴AC2=OCPC,解得PC=9,
∴OP=PC+OC=13.在Rt△PBC中,由勾股定理,得PB=![]() ,
,
∵AC=BC,OA=OE,即OC為△ABE的中位線.
∴OC=![]() BE,OC∥BE,∴BE=2OC=8.
BE,OC∥BE,∴BE=2OC=8.
∵BE∥OP,∴△DBE∽△DPO,
∴![]() ,即
,即![]() ,解得BD=
,解得BD=![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某學校開展“青少年科技創新比賽”活動,“喜洋洋”代表隊設計了一個遙控車沿直線軌道AC做勻速直線運動的模型.甲、乙兩車同時分別從A,B兩處出發,沿軌道到達C處,B在AC上,甲的速度是乙的速度的1.5倍,設t(分)后甲、乙兩遙控車與B處的距離分別為d1,d2,則d1,d2與t的函數關系如圖,試根據圖象解決下列問題:
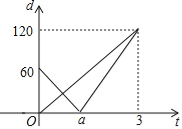
(1)填空:乙的速度v2= 米/分;
(2)寫出d1與t的函數關系式:
(3)若甲、乙兩遙控車的距離超過10米時信號不會產生相互干擾,試探求什么時間兩遙控車的信號不會產生相互干擾?
查看答案和解析>>
科目:初中數學 來源: 題型:
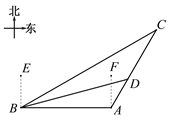
【題目】如圖,某天我國一艘海監船巡航到A港口正西方的B處時,發現在B的北偏東60°方向,相距150海里處的C點有一可疑船只正沿CA方向行駛,C點在A港口的北偏東30°方向上,海監船向A港口發出指令,執法船立即從A港口沿AC方向駛出,在D處成功攔截可疑船只,此時D點與B點的距離為75![]() 海里.
海里.
(1)求B點到直線CA的距離;
(2)執法船從A到D航行了多少海里?(![]() ≈1.414,
≈1.414,![]() ≈1.732,結果精確到0.1海里)
≈1.732,結果精確到0.1海里)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,長方形![]() 的邊
的邊![]() 在數軸上,
在數軸上,![]() 為原點,長方形
為原點,長方形![]() 的面積為12,
的面積為12,![]() 邊的長為3.
邊的長為3.
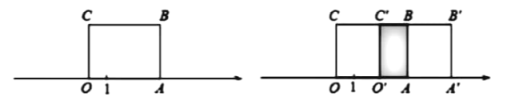
(1)數軸上點![]() 表示的數為________.
表示的數為________.
(2)將長方形![]() 沿數軸水平移動,移動后的長方形記為
沿數軸水平移動,移動后的長方形記為![]() ,設長方形
,設長方形![]() 移動的距離為
移動的距離為![]() ,移動后的長方形
,移動后的長方形![]() 與原長方形
與原長方形![]() 重疊部分的面積記為
重疊部分的面積記為![]() .
.
①當![]() 等于原長方形
等于原長方形![]() 面積的
面積的![]() 時,則點
時,則點![]() 的移動距離
的移動距離![]() _______,此時數軸上點
_______,此時數軸上點![]() 表示的數為_______.
表示的數為_______.
②![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上,且
上,且![]() 當點
當點![]() ,
,![]() 所表示的數互為相反數時,則
所表示的數互為相反數時,則![]() 的值為_______.
的值為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】怡然美食店的A、B兩種菜品,每份成本均為14元,售價分別為20元、18元,這兩種菜品每天的營業額共為1120元,總利潤為280元.
(1)該店每天賣出這兩種菜品共多少份?
(2)該店為了增加利潤,準備降低A種菜品的售價,同時提高B種菜品的售價,售賣時發現,A種菜品售價每降0.5元可多賣1份;B種菜品售價每提高0.5元就少賣1份,如果這兩種菜品每天銷售總份數不變,那么這兩種菜品一天的總利潤最多是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
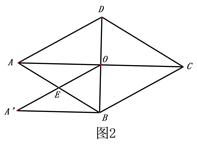
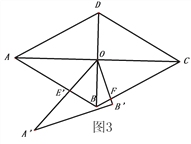
【題目】如圖1,菱形ABCD,AB=4,∠ADC=120o,連接對角線AC、BD交于點O,
(1)如圖2,將△AOD沿DB平移,使點D與點O重合,求平移后的△A′BO與菱形ABCD重合部分的面積.
(2)如圖3,將△A′BO繞點O逆時針旋轉交AB于點E′,交BC于點F,
①求證:BE′+BF=2,
②求出四邊形OE′BF的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A,B兩點在反比例函數y=![]() 的圖象上,C,D兩點在反比例函數y=
的圖象上,C,D兩點在反比例函數y=![]() 的圖象上,AC⊥x軸于點E,BD⊥x軸于點F,AC=2,BD=3,EF=
的圖象上,AC⊥x軸于點E,BD⊥x軸于點F,AC=2,BD=3,EF=![]() ,則k2-k1的值為( )
,則k2-k1的值為( )

A. 4 B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于任意有理數a,b,定義運算:a⊙b=a(a+b)﹣1,等式右邊是通常的加法、減法、乘法運算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)對于任意有理數m,n,請你重新定義一種運算“⊕”,使得5⊕3=20,寫出你定義的運算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知拋物線y=x2+bx+c過A,B,C三點,點A的坐標是(3,0),點C的坐標是(0,-3),動點P在拋物線上.
(1)b =_________,c =_________,點B的坐標為_____________;(直接填寫結果)
(2)是否存在點P,使得△ACP是以AC為直角邊的直角三角形?若存在,求出所有符合條件的點P的坐標;若不存在,說明理由;
(3)過動點P作PE垂直y軸于點E,交直線AC于點D,過點D作x軸的垂線.垂足為F,連接EF,當線段EF的長度最短時,求出點P的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com