
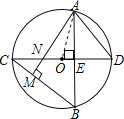
【題目】如圖,⊙O中,直徑CD⊥弦AB于E,AM⊥BC于M,交CD于N,連AD.AB=![]() ,ON=1,則⊙O的半徑長為_____________.
,ON=1,則⊙O的半徑長為_____________.
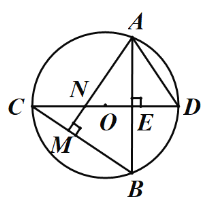
【答案】3
【解析】
先根據圓周角定理得出∠BAD=∠BCD,再由直角三角形的性質得出∠ANE=∠CNM,故可得出∠BCD=∠BAM,由全等三角形的判定定理得出△ANE≌△ADE,得到NE=ED,根據垂徑定理求出AE的長,設NE=![]() ,則OE=
,則OE=![]() ,NE=ED=
,NE=ED=![]() ,r=OD=OE+ED=
,r=OD=OE+ED=![]() ,連結AO,則AO=OD=
,連結AO,則AO=OD=![]() ,在Rt△AOE中根據勾股定理可得出
,在Rt△AOE中根據勾股定理可得出![]() 的值,進而得出結論.
的值,進而得出結論.
∵∠BAD與∠BCD是同弧所對的圓周角,
∴∠BAD=∠BCD,
∵AE⊥CD,AM⊥BC,
∴∠AMC=∠AEN=90°,
∵∠ANE=∠CNM,
∴∠BCD=∠BAM,
∴∠BAM=BAD,
在△ANE與△ADE中,
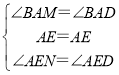 ,
,
∴△ANE≌△ADE,
∴NE=ED,
∵AB=![]() ,AE⊥CD,
,AE⊥CD,
∴AE=![]() AB =
AB =![]() ,
,
又∵ON=1,
∴設NE=![]() ,則OE=
,則OE=![]() ,NE=ED=
,NE=ED=![]() ,
,![]() ,
,
連結AO,
∴AO=OD=![]() ,
,
∵△AOE是直角三角形,AE=![]() ,,OE=
,,OE=![]() ,AO=
,AO=![]() ,
,
∴![]() ,即
,即![]() ,
,
整理得:![]() ,
,
解得:![]() (舍去),
(舍去),
∴![]() .
.
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】為迎接2020年第35屆全國青少年科技創新大賽,某學校舉辦了A:機器人;B:航模;C:科幻繪畫;D:信息學;E:科技小制作等五項比賽活動(每人限報一項),將各項比賽的參加人數繪制成如圖兩幅不完整的統計圖.
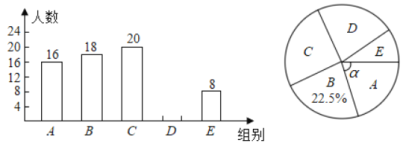
根據統計圖中的信息解答下列問題:
(1)本次參加比賽的學生人數是_________名;
(2)把條形統計圖補充完整;
(3)求扇形統計圖中表示機器人的扇形圓心角![]() 的度數;
的度數;
(4)在C組最優秀的3名同學(1名男生2名女生)和E組最優秀的3名同學(2名男生1名女生)中,各選1名同學參加上一級比賽,利用樹狀圖或表格,求所選兩名同學中恰好是1名男生1名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=3,BC=4,動點P從A點出發,按A→B→C的方向在AB和BC上移動,記PA=x,點D到直線PA的距離為y,則y關于x的函數圖象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某風景區內的公路如圖1所示,景區內有免費的班車,從入口處出發,沿該公路開往草甸,途中停靠塔林(上下車時間忽略不計).第一班車上午8點發車,以后每隔10分鐘有一班車從入口處發車.小聰周末到該風景區游玩,上午7:40到達入口處,因還沒到班車發車時間,于是從景區入口處出發,沿該公路步行25分鐘后到達塔林.離入口處的路程![]() (米)與時間
(米)與時間![]() (分)的函數關系如圖2所示.
(分)的函數關系如圖2所示.
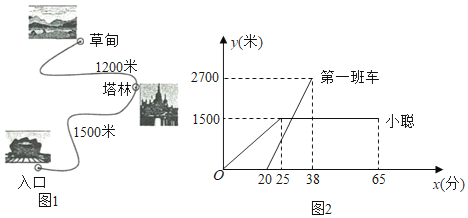
(1)求第一班車離入口處的路程![]() (米)與時間
(米)與時間![]() (分)的函數表達式.
(分)的函數表達式.
(2)求第一班車從人口處到達塔林所蓄的時間.
(3)小聰在塔林游玩40分鐘后,想坐班車到草甸,則小聘聰最早能夠坐上第幾班車?如果他坐這班車到草甸,比他在塔林游玩結束后立即步行到草甸提早了幾分鐘?(假設每一班車速度均相同,小聰步行速度不變)
查看答案和解析>>
科目:初中數學 來源: 題型:
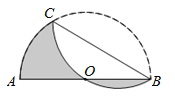
【題目】如圖,AB是半圓O的直徑,且AB=6cm,點C為半圓上的一點,將此半圓沿BC所在的直線折疊,若圓弧BC恰好過圓心O,則圖中陰影部分的面積是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“互聯網+”時代,網上購物備受消費者青睞.某網店專售一種商品,其成本為每件![]() 元,已知銷售過程中,銷售單價不低于成本單價,且物價部門規定這種商品的獲利不得高于
元,已知銷售過程中,銷售單價不低于成本單價,且物價部門規定這種商品的獲利不得高于![]() .據市場調查發現,月銷售量
.據市場調查發現,月銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元)之間的函數關系如表:
(元)之間的函數關系如表:
銷售單價 | 65 | 70 | 75 | 80 | ··· |
月銷售量 | 475 | 450 | 425 | 400 | ··· |
![]() 請根據表格中所給數據,求出
請根據表格中所給數據,求出![]() 關于
關于![]() 的函數關系式;
的函數關系式;
![]() 設該網店每月獲得的利潤為
設該網店每月獲得的利潤為![]() 元,當銷售單價為多少元時,每月獲得的利潤最大,最大利潤是多少?
元,當銷售單價為多少元時,每月獲得的利潤最大,最大利潤是多少?
![]() 該網店店主熱心公益事業,決定每月從利潤中捐出
該網店店主熱心公益事業,決定每月從利潤中捐出![]() 元資助貧困學生.為了保證捐款后每月利潤不低于
元資助貧困學生.為了保證捐款后每月利潤不低于![]() 元,且讓消費者得到最大的實惠,該如何確定該商品的銷售單價?
元,且讓消費者得到最大的實惠,該如何確定該商品的銷售單價?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.為了解一批電池的使用壽命,應采用全面調查的方式
B.數據![]() ,
,![]() ,...,
,...,![]() 的平均數是
的平均數是![]() ,方差是
,方差是![]() ,則數據
,則數據![]() ,
,![]() ,...,
,...,![]() 的平均數是
的平均數是![]() ,方差是
,方差是![]()
C.通過對甲、乙兩組學生數學成績的跟蹤調查,整理計算得到甲、乙兩組數據的方差為![]() ,
,![]() ,則乙數據較為穩定
,則乙數據較為穩定
D.為了解官渡區九年級![]() 多名學生的視力情況,從中隨機選取
多名學生的視力情況,從中隨機選取![]() 名學生的視力情況進行分析,則選取的樣本容量為
名學生的視力情況進行分析,則選取的樣本容量為![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一艘快艇從O港出發,向西北方向行駛到M處,然后向正東行駛到N處,再向西南方向行駛,共經過1.5小時回到O港,已知快艇的速度是每小時50海里,則M,N之間的距離是( )海里

A.75![]() ﹣75B.
﹣75B.![]() C.75
C.75![]() D.50
D.50![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,草原上有A,B,C三個互通公路的奶牛養殖基地,B與C之間距離為100千米,C在B的正北方,A在C的南偏東60°方向且在B的北偏東30°方向.A地每年產奶3萬噸;B地有奶牛9000頭,平均每頭牛的年產奶量為3噸;C地養了三種奶牛,其中黑白花牛的頭數占20%,三河牛的頭數占35%,其他情況反映在圖(2),圖(3)中.

(1)通過計算補全圖(3);
(2)比較B地與C地中,哪一地平均每頭牛的年產奶量更高?
(3)如果從B,C兩地中選擇一處建設一座工廠解決三個基地的牛奶加工問題,當運送一噸牛奶每千米的費用都為1元,那么從節省運費的角度考慮,應在何處建設工廠?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com