
【題目】已知,正方形ABCD的邊長為4,點E是對角線BD延長線上一點,AE=BD.將△ABE繞點A順時針旋轉α度(0°<α<360°)得到△AB′E′,點B、E的對應點分別為B′、E′.
(1)如圖1,當α=30°時,求證:B′C=DE;
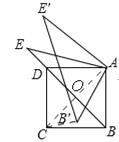
(2)連接B′E、DE′,當B′E=DE′時,請用圖2求α的值;
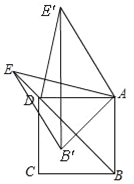
(3)如圖3,點P為AB的中點,點Q為線段B′E′上任意一點,試探究,在此旋轉過程中,線段PQ長度的取值范圍為 .

【答案】(1)證明見解析(2)45°(3)![]() ≤PQ≤4
≤PQ≤4![]() +2
+2
【解析】試題分析:(1)、連接AC,B′C,根據正方形的性質得出得出AC=AE=2OA,根據Rt△AOE的性質得出∠E=30°,然后結合旋轉圖形的性質得出△ADE和△AB′C全等,從而得出答案;(2)、根據旋轉圖形的性質得出△AEB′和△AE′D全等,從而得出∠DAE′=∠EAB′,然后結合旋轉圖形的性質得出∠EAE′=∠BAB′,從而得到∠BAB′=∠DAB′,最后根據∠BAB′+∠DAB′=90°得出答案;(3)、點P作PM⊥BE,∵AB=4,點P是AB中點,根據BP=2得出PM=![]() ;在旋轉過程中,△ABE在旋轉到點E在BA的延長線時,點Q和點E重合,然后求出PQ的長度,從而得出取值范圍.
;在旋轉過程中,△ABE在旋轉到點E在BA的延長線時,點Q和點E重合,然后求出PQ的長度,從而得出取值范圍.
試題解析:(1)如圖,連接AC,B′C, ∵四邊形ABCD是正方形,
∴AB=AD,AC⊥BD,AC=BD=2OA,∠CAB=ADB=45°, ∵AE=BD, ∴AC=AE=2OA,
在Rt△AOE中,∠AOE=90°,AE=2OA, ∴∠E=30°,
∴∠DAE=∠ADB﹣∠E=45°﹣30°=15°, 由旋轉有,AD=AB=AB′∠BAB′=30°
∴∠DAE=15°,
在△ADE和△AB′C中,  , ∴△ADE≌△AB′C,∴DE=B′C,
, ∴△ADE≌△AB′C,∴DE=B′C,
(2)如圖,
由旋轉得,AB′=AB=AD,AE′=AE,
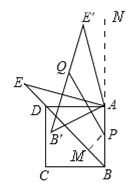
在△AEB′和△AE′D中, 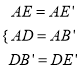 ,∴△AEB′≌△AE′D,∴∠DAE′=∠EAB′,
,∴△AEB′≌△AE′D,∴∠DAE′=∠EAB′,
∴∠EAE′=∠DAB′,由旋轉得,∠EAE′=∠BAB′,∴∠BAB′=∠DAB′,
∵∠BAB′+∠DAB′=90°,∴α=∠BAB′=45°,
(3)如圖,由點到直線的距離,過點P作PM⊥BE,∵AB=4,點P是AB中點,
∴BP=2,∴PM=![]() ,
,
在旋轉過程中,△ABE在旋轉到點E在BA的延長線時,點Q和點E重合,
∴AQ=AE=BQ=4![]() ∴PQ=AQ+AP=4
∴PQ=AQ+AP=4![]() +2,
+2,
故答案為![]() ≤PQ≤4
≤PQ≤4![]() +2.
+2.


 學業測評一課一測系列答案
學業測評一課一測系列答案科目:初中數學 來源: 題型:
【題目】在平行四邊形ABCD中,點A1 , A2 , A3 , A4和C1 , C2 , C3 , C4分別AB和CD的五等分點,點B1 , B2和D1 , D2分別是BC和DA的三等分點,已知四邊形A4B2C4D2的面積為1,則平行四邊形ABCD面積為( )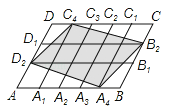
A.2
B.![]()
C.![]()
D.15
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】1納米=10-9米,將50納米用科學記數法表示為( )
A. 50×10-9米B. 5×10-9米C. 0.5×10-9米D. 5×10-8米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校規定學生的學期數學成績滿分為100分,其中平時學習成績占30%,期末卷面成績占70%,小明的兩項成績(百分制)依次是80分,90分,則小明這學期的數學成績是( )
A. 83分B. 86分C. 87分D. 92.4分
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工人若每小時生產38個零件,在規定時間內還有15個不能完成,若每小時生產42個零件,則可以超額完成5個,問:規定時間是多少?設規定時間為x小時,則可列方程為( )
A. 38x﹣15=42x+5 B. 38x+15=42x﹣5 C. 42x+38x=15+5 D. 42x﹣38x=15﹣5
查看答案和解析>>
科目:初中數學 來源: 題型:
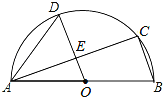
【題目】如圖,AB是半圓O的直徑,C、D是半圓O上的兩點,且OD∥BC,OD與AC交于點E.
(1)若∠B=72°,求∠CAD的度數;
(2)若AB=13,AC=12,求DE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com