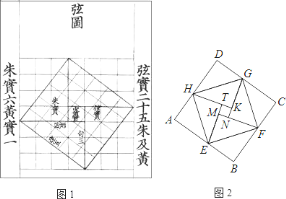
【題目】漢代數學家趙爽為了證明勾股定理，創制了一幅“弦圖”，后人稱其為“趙爽弦圖”（如圖
）．圖
是由弦圖變化得到的，它由八個全等的直角三角形拼接而成，記圖中正方形
、正方形
、正方形
的面積分別為
、
、
．若
，則的值是（ ）
A. 
B. 
C. 
D. 
科目：初中數學 來源： 題型：
【題目】我校初三學子在不久前結束的體育中考中取得滿意成績，贏得2016年中考開門紅．現隨機抽取了部分學生的成績作為一個樣本，按A（滿分）、B（優秀）、C（良好）、D（及格）四個等級進行統計，并將統計結果制成如下2幅不完整的統計圖，如圖，請你結合圖表所給信息解答下列問題： 
（1）將折線統計圖在圖中補充完整；此次調查共隨機抽取了名學生，其中學生成績的中位數落在等級；
（2）為了今后中考體育取得更好的成績，學校決定分別從成績為滿分的男生和女生中各選一名參加“經驗座談會”，若成績為滿分的學生中有4名女生，且滿分的男、女生中各有2名體育特長生，請用列表或畫樹狀圖的方法求出所選的兩名學生剛好都不是體育特長生的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在菱形ABCD中，∠ABC=60°，E是對角線AC上任意一點，F是線段BC延長線上一點，且CF=AE，連接BE、EF．
（1）如圖1，當E是線段AC的中點，且AB=2時，求△ABC的面積；
（2）如圖2，當點E不是線段AC的中點時，求證：BE=EF；
（3）如圖3，當點E是線段AC延長線上的任意一點時，（2）中的結論是否成立？若成立，請給予證明；若不成立，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了了解2014年某地區10萬名大、中、小學生50米跑成績情況，教育部門從這三類學生群體中各抽取了10%的學生進行檢測，整理樣本數據，并結合2010年抽樣結果，得到下列統計圖：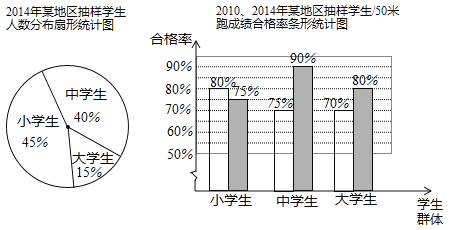
（1）本次檢測抽取了大、中、小學生共 名，其中小學生 名；
（2）根據抽樣的結果，估計2014年該地區10萬名大、中、小學生中，50米跑成績合格的中學生人數為 名；
（3）比較2010年與2014年抽樣學生50米跑成績合格率情況，寫出一條正確的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】課間，小聰拿著老師的等腰直角三角板玩，不小心掉到兩墻之間（如圖），
，
，從三角板的刻度可知
，小聰很快就知道了砌墻磚塊的厚度的平方（每塊磚的厚度相等）為________
．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，點A(2，0)，B(0，4)，作△BOC，使△BOC與△ABO全等，則點C坐標為________________________________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，O為原點，點A（﹣2，0），點B（0，2），點E，點F分別為OA，OB的中點．若正方形OEDF繞點O順時針旋轉，得正方形OE′D′F′，記旋轉角為α． 
（1）如圖①，當α=90°時，求AE′，BF′的長；
（2）如圖②，當α=135°時，求證AE′=BF′，且AE′⊥BF′；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線y=ax2+bx+c（a≠0）經過A（﹣1，0），B（4，0），C（0，2）三點． 
（1）求這條拋物線的解析式；
（2）E為拋物線上一動點，是否存在點E，使以A、B、E為頂點的三角形與△COB相似？若存在，試求出點E的坐標；若不存在，請說明理由；
（3）若將直線BC平移，使其經過點A，且與拋物線相交于點D，連接BD，試求出∠BDA的度數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
