
【題目】如圖,在平面直角坐標系中,二次函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
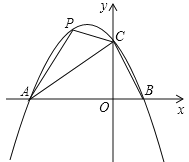
(1)求這個二次函數的解析式;
(2)點![]() 是直線
是直線![]() 上方的拋物線上一動點,是否存在點
上方的拋物線上一動點,是否存在點![]() ,使得
,使得![]() 的面積最大?若存在,求出點
的面積最大?若存在,求出點![]() 的坐標;若不存在,說明理由;
的坐標;若不存在,說明理由;
(3)點![]() 是直線
是直線![]() 上方的拋物線上一動點,過點
上方的拋物線上一動點,過點![]() 作
作![]() 軸于點
軸于點![]() .是否存在點
.是否存在點![]() ,使以點
,使以點![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,直接寫出點
相似?若存在,直接寫出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
【答案】(1)![]() ;(2)存在,點
;(2)存在,點![]() ;(3)存在,
;(3)存在,![]() ,
,![]() .
.
【解析】
(1)把點A、B的坐標代入二次函數解析式,利用待定系數法求二次函數解析式解答;
(2)連接![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,
,![]() 軸于點
軸于點![]() ,設點
,設點![]() 的坐標為
的坐標為![]() ,得出
,得出![]() ,從而推出
,從而推出![]() ,即可推出當
,即可推出當![]() 時,
時,![]() 的面積最大,從而求出點
的面積最大,從而求出點![]() 的坐標.
的坐標.
(3)設點E的橫坐標為c,表示出BE、QE,然后根據相似三角形對應邊成比例,分OA和BE,OA和QE是對應邊兩種情況列出比例式求解即可.
(1)由拋物線![]() 過點
過點![]() ,
,![]() ,
,
則![]() ,解得
,解得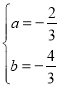 .
.
![]() 二次函數的解析式為
二次函數的解析式為![]() .
.
(2)存在.如圖,連接![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,
,![]() 軸于點
軸于點![]() .
.
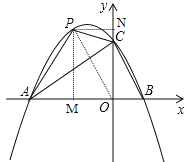
設點![]() 的坐標為
的坐標為![]() ,則
,則![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() 當
當![]() 時,
時,![]() ,
,
![]() .
.
![]()
![]()
![]()
![]() .
.
![]() ,
,
![]() 當
當![]() 時,
時,![]() 有最大值.
有最大值.
此時![]() .
.
![]() 存在點
存在點![]() ,使
,使![]() 的面積最大.
的面積最大.
(3)存在點![]() ,坐標為
,坐標為![]() ,
,![]() .
.
理由如下:設點E的橫坐標為c,則點Q的坐標為![]() BE=1-c,
BE=1-c,
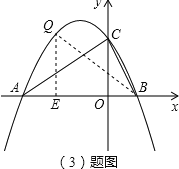
①OA和BE是對應邊時,∵△BEQ∽△AOC,
∴![]() ,
,
即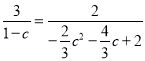 ,
,
整理得,c2+c-2=0,
解得c1=-2,c2=1(舍去),
此時,![]() ,
,
點Q(-2,2);
②OA和QE是對應邊時,∵△QEB∽△AOC,
∴![]() ,
,
即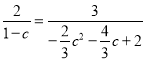 ,
,
整理得,4c2-c-3=0,
解得![]() ,c2=1(舍去),
,c2=1(舍去),
此時,![]() ,
,
點![]() ;
;
綜上所述,存在點![]() ,
,![]() 使以點B、Q、E為頂點的三角形與△AOC相似.
使以點B、Q、E為頂點的三角形與△AOC相似.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:初中數學 來源: 題型:
【題目】設AD為∠BAC的平分線,AB=8,AC=10,AD=6,E為AC上一點,AE=2,M為AE的中點,N為BC的中點,則MN=( )
A.5B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】博文書店舉行購書優惠活動:
①一次性購書不超過100元,不享受打折優惠;
②一次性購書超過100元但不超過200元一律打九折;
③一次性購書200元以上一律打七折.
小麗在這次活動中,兩次購書總共付款229.4元,第二次購書原價是第一次購書原價的3倍,那么小麗這兩次購書原價的總和是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
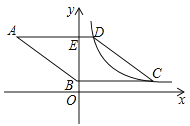
【題目】如圖,菱形![]() 的邊
的邊![]() 軸,垂足為點
軸,垂足為點![]() ,頂點
,頂點![]() 在第二象限,頂點
在第二象限,頂點![]() 在
在![]() 軸的正半軸上,反比例函數
軸的正半軸上,反比例函數![]() (
(![]() ,
,![]() )的圖象同時經過頂點
)的圖象同時經過頂點![]() ,
,![]() ,若點
,若點![]() 的橫坐標為10,
的橫坐標為10,![]() ,則
,則![]() 的值為_______.
的值為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
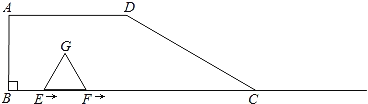
【題目】如圖,四邊形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°,點E、F同時從B點出發,沿射線BC向右勻速移動.已知F點移動速度是E點移動速度的2倍,以EF為一邊在CB的上方作等邊△EFG.設E點移動距離為x(0<x<6).
(1)點G在四邊形ABCD的邊上時,x= ;點F與點C重合時,x= ;
(2)求出使△DFC成為等腰三角形的x的值;
(3)求△EFG與四邊形ABCD重疊部分的面積y與x之間的函數關系式,并直接寫出y的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知點A,B,C是⊙O上的三點,以AB,BC為鄰邊作ABCD,延長AD,交⊙O于點E,過點A作CE的平行線,交CD的延長線于F.
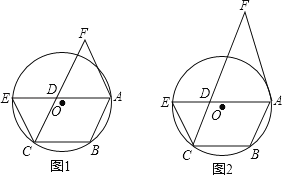
(1)求證:FD=FA;
(2)如圖2,連接AC,若∠F=40°,且AF恰好是⊙O的切線,求∠CAB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BD是邊長為1的正方形ABCD的對角線,BE平分∠DBC交DC于點E,延長BC到點F,使CF=CE,連接DF,交BE的延長線于點G.
(1)求證:△BCE≌△DCF;
(2)求CF的長。

查看答案和解析>>
科目:初中數學 來源: 題型:
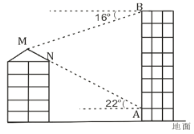
【題目】如圖,小明在商城二樓地板![]() 處發現對五層居民樓頂防雨棚一側斜面
處發現對五層居民樓頂防雨棚一側斜面![]() 與點
與點![]() 在一條直線上,此時測得
在一條直線上,此時測得![]() ,
,![]() 仰角是
仰角是![]() ,上到九樓在地板邊沿
,上到九樓在地板邊沿![]() 點測得居民樓頂斜面頂端
點測得居民樓頂斜面頂端![]() 點俯角是
點俯角是![]() ,已知商城每層樓高
,已知商城每層樓高![]() 米,居民樓每層樓高
米,居民樓每層樓高![]() 米,試計算居民樓頂防雨棚一側斜面
米,試計算居民樓頂防雨棚一側斜面![]() 的長度.(結果保留精確到
的長度.(結果保留精確到![]() 米)(參考數據:
米)(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com