
如圖,在平面直角坐標系xOy中,一動直線l從y軸出發,以每秒1個單位長度的速度沿x軸向右平移,直線l與直線y=x相交于點P,以OP為半徑的⊙P與x軸正半軸交于點A,與y軸正半軸交于點B.設直線l的運動時間為t秒.

(1)填空:當t=1時,⊙P的半徑為 ,OA= ,OB= ;
(2)若點C是坐標平面內一點,且以點O、P、C、B為頂點的四邊形為平行四邊形.
①請你直接寫出所有符合條件的點C的坐標;(用含t的代數式表示)
②當點C在直線y=x上方時,過A、B、C三點的⊙Q與y軸的另一個交點為點D,連接DC、DA,試判斷△DAC的形狀,并說明理由.
解:(1)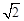 ;2;2。
;2;2。
(2)①符合條件的點C有3個,分別為C1(t,3t)、C2(-t,t)、C3(t,-t)。
②△DAC是等腰直角三角形。理由見解析
【解析】
試題分析:(1)利用垂徑定理、等腰直角三角形的性質求解。
(2)①本問關鍵是畫出符合條件的圖形,總共有3種情況,符合條件的點C有3個,如圖1,
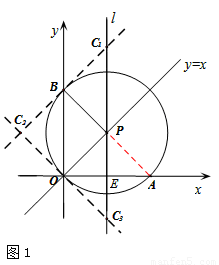
連接PA,
∵∠AOB=90°,由圓周角定理可知,AB為圓的直徑,點A、P、B共線。
∵圓心P在直線y=x上,∴∠POA=∠POB=45°。
又∵PO=PA=PB,∴△POB與△POA均為等腰直角三角形。
設動直線l與x軸交于點E,
則有E(t,0),P(t,t),B(0,2t)。
∵OBPC1為平行四邊形,∴C1P=OB=2t,C1E=C1P+PE=2t+t=3t,
∴C1(t,3t)。
同理可求得:C3(t,-t)。
∵OPBC2為平行四邊形,且PB=PO,∠OPB=90°,
∴ OPBC2為正方形,其對角線OB位于y軸上,則點P與點C2關于x軸對稱。
OPBC2為正方形,其對角線OB位于y軸上,則點P與點C2關于x軸對稱。
∴C2(-t,t)。
∴符合條件的點C有3個,分別為C1(t,3t)、C2(-t,t)、C3(t,-t)。
②正確作出圖形,找到線段CD與AD之間的關聯,這就是Rt△DCE∽Rt△ADO,通過計算可知其相似比為1,即兩個三角形全等,從而得到CD=AD,△DAC為等腰直角三角形。本問符合條件的點C有2個,因此存在兩種情形,分別如答圖2和答圖3所示。
△DAC是等腰直角三角形。理由如下:
當點C在第一象限時,如圖2,連接DA、DC、PA、AC,
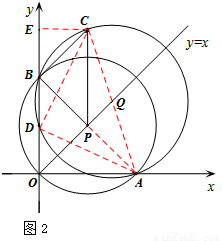
由(2)可知,點C的坐標為(t,3t),
由點P坐標為(t,t),點A坐標為(2t,0),點B坐標為(0,2t),可知OA=OB=2t,△OAB是等腰直角三角形。
又PO=PB,進而可得△OPB也是等腰直角三角形,
則∠POB=∠PBO=45°。
∵∠AOB=90°,∴AB為⊙P的直徑。
∴A、P、B三點共線。
又∵BC∥OP,∴∠CBE=∠POB=45°。
∴∠ABC=180°-∠CBE-∠PBO=90°。∴AC為⊙Q的直徑。∴DA⊥DC。
∴∠CDE+∠ADO=90°。
過點C作CE⊥y軸于點E,則有∠DCE+∠CDE=90°,∴∠ADO=∠DCE。
∴Rt△DCE∽Rt△ADO,∴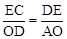 ,即
,即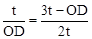 ,解得OD=t或OD=2t。
,解得OD=t或OD=2t。
依題意,點D與點B不重合,∴舍去OD=2t,只取OD=t。
∴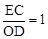 ,即相似比為1,此時兩個三角形全等,則DC=AD。
,即相似比為1,此時兩個三角形全等,則DC=AD。
∴△DAC是等腰直角三角形。
當點C在第二象限時,如圖3,同上可證△DAC也是等腰直角三角形。
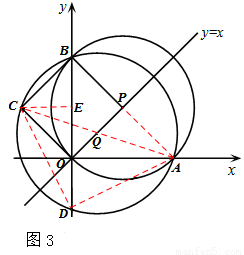
綜上所述,當點C在直線y=x上方時,△DAC必為等腰直角三角形。


科目:初中數學 來源: 題型:
 如圖,在平面直角坐標中,四邊形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,點P為x軸上的一個動點,但是點P不與點0、點A重合.連接CP,D點是線段AB上一點,連接PD.
如圖,在平面直角坐標中,四邊形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,點P為x軸上的一個動點,但是點P不與點0、點A重合.連接CP,D點是線段AB上一點,連接PD.| BD |
| AB |
| 5 |
| 8 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•渝北區一模)如圖,在平面直角坐標xoy中,以坐標原點O為圓心,3為半徑畫圓,從此圓內(包括邊界)的所有整數點(橫、縱坐標均為整數)中任意選取一個點,其橫、縱坐標之和為0的概率是
(2012•渝北區一模)如圖,在平面直角坐標xoy中,以坐標原點O為圓心,3為半徑畫圓,從此圓內(包括邊界)的所有整數點(橫、縱坐標均為整數)中任意選取一個點,其橫、縱坐標之和為0的概率是| 5 |
| 29 |
| 5 |
| 29 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在平面直角坐標xOy中,已知點A(-5,0),P是反比例函數y=
如圖,在平面直角坐標xOy中,已知點A(-5,0),P是反比例函數y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:
 ∠COA=45°,動點P從點O出發,在梯形OABC的邊上運動,路徑為O→A→B→C,到達點C時停止.作直線CP.
∠COA=45°,動點P從點O出發,在梯形OABC的邊上運動,路徑為O→A→B→C,到達點C時停止.作直線CP.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com