
【題目】如圖,長度為5的動線段AB分別與坐標系橫軸、縱軸的正半軸交于點A、點B,點O和點C關于AB對稱,連接CA、CB,過點C作x軸的垂線段CD,交x軸于點D
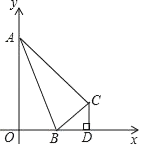
(1)移動點A,發現在某一時刻,△AOB和以點B、D、C為頂點的三角形相似,求這一時刻點C的坐標;
(2)移動點A,當![]() 時求點C的坐標.
時求點C的坐標.
【答案】(1)點![]() 的坐標為
的坐標為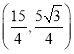 ;(2)
;(2)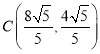 .
.
【解析】
(1)根據軸對稱的性質得:AB是OC的垂直平分線,由垂直平分線的性質得:OB=BC,OA=AC,△AOB和以點B、D、C為頂點的三角形相似,存在兩種情況:
①當∠ABO=∠CBD時,②當∠ABO=∠BCD時,根據角的關系分別計算點C的坐標即可;
(2)先根據三角函數定義求OB=![]() ,OA=2
,OA=2![]() ,利用面積法得OG和OC的長,根據等角的三角函數可知:OG=2BG,證明△BGO∽△CDO,列比例式可得結論.
,利用面積法得OG和OC的長,根據等角的三角函數可知:OG=2BG,證明△BGO∽△CDO,列比例式可得結論.
(1)連接![]() ,交
,交![]() 于
于![]() ,
,
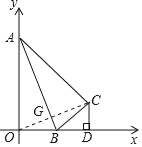
∵點![]() 和點
和點![]() 關于
關于![]() 對稱,
對稱,
![]() 是
是![]() 的垂直平分線,
的垂直平分線,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 和以點
和以點![]() 為頂點的三角形相似,存在兩種情況:
為頂點的三角形相似,存在兩種情況:
①當![]() 時,
時,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
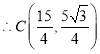 ;
;
②當![]() 時,
時,![]() ,
,
![]() ,
,
![]() 軸,
軸,
![]() 軸,此種情況不成立;
軸,此種情況不成立;
綜上所述,![]() 和以點
和以點![]() 為頂點的三角形相似,這一時刻點
為頂點的三角形相似,這一時刻點![]() 的坐標為
的坐標為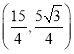 ;
;
(2)![]() ,
,
設![]() ,則
,則![]() ,
,
![]() ,
,
![]() 或
或![]() (舍),
(舍),
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
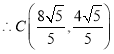 .
.


科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c經過A(﹣1,0)、B(5,0)、C(0,﹣5)三點.
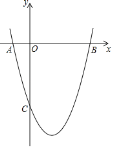
(1)求拋物線的解析式和頂點坐標;
(2)當0<x<5時,y的取值范圍為 ;
(3)點P為拋物線上一點,若S△PAB=21,直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】長沙市計劃聘請甲、乙兩個工程隊對桂花公園進行綠化.已知甲隊每天能完成綠化的面積是乙隊的2倍;若兩隊分別各完成300m2的綠化時,甲隊比乙隊少用3天.

(1)求甲、乙兩工程隊每天能完成的綠化的面積;
(2)該項綠化工程中有一塊長為20m,寬為8m的矩形空地,計劃在其中修建兩塊相同的矩形綠地,它們的面積之和為56m2,兩塊綠地之間及周邊留有寬度相等的人行通道(如圖所示),問人行通道的寬度是多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,△ABC是等邊三角形,點D、E分別在BC,AC且BD=CE,AD、BE相交于點M,

求證:(1)△AME∽△BAE;(2)BD2=AD×DM.
查看答案和解析>>
科目:初中數學 來源: 題型:
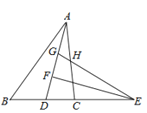
【題目】如圖,在![]() 中,4AB=5AC,AD為
中,4AB=5AC,AD為![]() 的角平分線,點E在BC的延長線上,
的角平分線,點E在BC的延長線上,![]() 于點F,點G在AF上,FG=FD,連接EG交AC于點H,若點H是AC的中點,則
于點F,點G在AF上,FG=FD,連接EG交AC于點H,若點H是AC的中點,則![]() 的值為___________
的值為___________
查看答案和解析>>
科目:初中數學 來源: 題型:
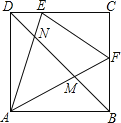
【題目】如圖,正方形ABCD的邊長為2,點E,F分別是DC和BC兩邊上的動點且始終保持∠EAF=45°,連接AE與AF交DB于點N,M.下列結論:①△ADM∽△NBA;②△CEF的周長始終保持不變其值是4;③AE×AM=AF×AN;④DN2+BM2=NM2.其中正確的結論是( )
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在下列網格圖中,每個小正方形的邊長均為1個單位.在Rt△ABC中,∠C=90°,AC=3,BC=2.
(1)試在圖中畫出將△ABC以B為旋轉中心,沿順時針方向旋轉90°后的圖形△A1BC1;
(2)若點B的坐標為(-1,-4),點C的坐標為(-3,-4),試在圖中畫出直角坐標系,并寫出點A的坐標;
(3)根據(2)的坐標系作出與△ABC關于原點對稱的圖形△A2B2C2.

查看答案和解析>>
科目:初中數學 來源: 題型:
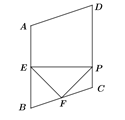
【題目】如圖,在菱形ABCD中,∠A=100°,E,F分別是邊AB和BC的中點,EP⊥CD于點P,則∠FPC=( )
A. 55°B. 65°C. 50°D. 45°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com