
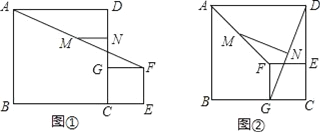
【題目】如圖①,C為線段BE上的一點,分別以BC和CE為邊在BE的同側作正方形ABCD和正方形CEFG,M、N分別是線段AF和GD的中點,連接MN
(1)線段MN和GD的數量關系是_____,位置關系是_____;
(2)將圖①中的正方形CEFG繞點C逆時針旋轉90°,其他條件不變,如圖②,(1)的結論是否成立?說明理由;
(3)已知BC=7,CE=3,將圖①中的正方形CEFG繞點C旋轉一周,其他條件不變,直接寫出MN的最大值和最小值.
【答案】 MN=![]() DG,MN⊥DG; (1)的結論仍然成立.
DG,MN⊥DG; (1)的結論仍然成立.
【解析】(1)連接FN并延長,與AD交于點S,如圖①,易證△SDN≌△FGN,則有DS=GF,SN=FN,然后運用三角形中位線定理就可解決問題;
(2)過點M作MT⊥DC于T,過點M作MR⊥BC于R,連接FC、MD、MG,如圖②,根據平行線分線段成比例可得BR=GR=![]() BG,DT=ET=
BG,DT=ET=![]() DE,根據梯形中位線定理可得MR=
DE,根據梯形中位線定理可得MR=![]() (FG+AB),MT=
(FG+AB),MT=![]() (EF+AD),從而可得MR=MT,RG=TD,由此可得△MRG≌△MTD,則有MG=MD,∠RMG=∠TMD,則有∠RMT=∠GMD,進而可證到△DMG是等腰直角三角形,然后根據等腰三角形的性質和直角三角形斜邊上的中線等于斜邊的一半,就可解決問題;
(EF+AD),從而可得MR=MT,RG=TD,由此可得△MRG≌△MTD,則有MG=MD,∠RMG=∠TMD,則有∠RMT=∠GMD,進而可證到△DMG是等腰直角三角形,然后根據等腰三角形的性質和直角三角形斜邊上的中線等于斜邊的一半,就可解決問題;
(3)連接GM到點P,使得PM=GM,延長GF、AD交于點Q,連接AP,DP,DM如圖③,易證△APD≌△CGD,則有PD=DG,根據等腰三角形的性質可得DM⊥PG,根據直角三角形斜邊上的中線等于斜邊的一半可得MN=![]() DG.要求MN的最大值和最小值,只需求DG的最大值和最小值,由GC=CE=3可知點G在以點C為圓心,3為半徑的圓上,再由DC=BC=7,就可求出DG的最大值和最小值.
DG.要求MN的最大值和最小值,只需求DG的最大值和最小值,由GC=CE=3可知點G在以點C為圓心,3為半徑的圓上,再由DC=BC=7,就可求出DG的最大值和最小值.
解:(1)連接FN并延長,與AD交于點S,如圖①.
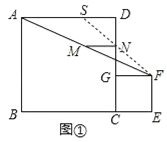
∵四邊形ABCD和四邊形EFGC都是正方形,
∴∠D=90°,AD=DC,GC=GF,AD∥BE∥GF,
∴∠DSN=∠GFN.
在△SDN和△FGN中,
∠DSN=∠GFN,∠SND=∠FNG,DN=GN,,
∴△SDN≌△FGN,
∴DS=GF,SN=FN.
∵AM=FM,
∴MN∥AS,MN=![]() AS,
AS,
∴∠MNG=∠D=90°,
MN=![]() (AD﹣DS)=
(AD﹣DS)=![]() (DC﹣GF)=
(DC﹣GF)=![]() (DC﹣GC)=
(DC﹣GC)=![]() DG.
DG.
故答案為MN=![]() DG,MN⊥DG;
DG,MN⊥DG;
(2)(1)的結論仍然成立.
理由:過點M作MT⊥DC于T,過點M作MR⊥BC于R,連接FC、MD、MG,如圖②,
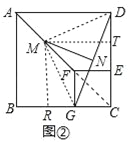
則A、F、C共線,MR∥FG∥AB,MT∥EF∥AD.
∵AM=FM,
∴BR=GR=![]() BG,DT=ET=
BG,DT=ET=![]() DE,
DE,
∴MR=![]() (FG+AB),MT=
(FG+AB),MT=![]() (EF+AD).
(EF+AD).
∵四邊形ABCD和四邊形EFGC都是正方形,
∴FG=GC=EC=EF,AB=BC=DC=AD,
∴MR=MT,RG=TD.
在△MRG和△MTD中,
MR=MT,∠MRG=∠MTD,RG=TD,
∴△MRG≌△MTD,
∴MG=MD,∠RMG=∠TMD,
∴∠RMT=∠GMD.
∵∠MRC=∠RCT=∠MTC=90°,
∴四邊形MRCT是矩形,
∴∠RMT=90°,
∴∠GMD=90°.
∵MG=MD,∠GMD=90°,DN=GN,
∴MN⊥DG,MN=![]() DG.
DG.
(3)延長GM到點P,使得PM=GM,延長GF、AD交于點Q,連接AP,DP,DM如圖③,
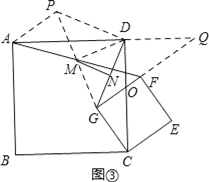
在△AMP和△FMG中,
AM=FM,∠AMP=∠FMG,PM=GM,
∴△AMP≌△FMG,
∴AP=FG,∠APM=∠FGM,
∴AP∥GF,
∴∠PAQ=∠Q,
∵∠DOG=∠ODQ+∠Q=∠OGC+∠GCO,
∠ODQ=∠OGC=90°,
∴Q=∠GCO,
∴∠PAQ=∠GCO.
∵四邊形ABCD和四邊形EFGC都是正方形,
∴DA=DC,GF=GC,
∴AP=CG.
在△APD和△CGD中,
AP=CG,∠PAD=∠GCD,AD=CD,
∴△APD≌△CGD,
∴PD=DG.
∵PM=GM,
∴DM⊥PG.
∵DN=GN,
∴MN=![]() DG.
DG.
∵GC=CE=3,
∴點G在以點C為圓心,3為半徑的圓上,
∵DC=BC=7,
∴DG的最大值為7+3=10,最小值為7﹣3=4,
∴MN的最大值為5,最小值為2.
“點睛”本題主要考查了全等三角形的判定與性質、正方形的性質、三角形中位線定理、平行線分階段成比例、梯形中位線定理、等腰直角三角形的判定與性質、等腰三角形的性質、直角三角形斜邊上的中線等于斜邊的一半、圓的定義、平行線的判定與性質等知識,綜合性強,有一定的難度,證到△DMG是等腰直角三角形是解決第(2)小題的關鍵,證到MN=![]() DG是解決第(3)小題的關鍵.
DG是解決第(3)小題的關鍵.


 智慧課堂密卷100分單元過關檢測系列答案
智慧課堂密卷100分單元過關檢測系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=60°,DE是斜邊AC的中垂線,分別交AB,AC于D,E兩點.若BD=2,則AC的長是( )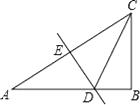
A.4
B.4 ![]()
C.8
D.8 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABD中,AB=AD,以AB為直徑的⊙F交BD于點C,交AD于點E,CG⊥AD于點G,連接FE,FC.
(1)求證:GC是⊙F的切線;
(2)填空:
①若∠BAD=45°,AB=2![]() ,則△CDG的面積為_____.
,則△CDG的面積為_____.
②當∠GCD的度數為_____時,四邊形EFCD是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是等腰梯形,∠ABC=60°,若其四邊滿足長度的眾數為5,平均數為 ![]() ,上、下底之比為1:2,則BD的長是( ).
,上、下底之比為1:2,則BD的長是( ).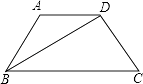
A.5
B.5 ![]()
C.3 ![]()
D.3 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com