
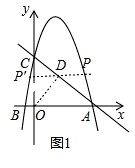
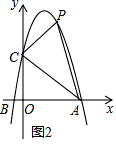
【題目】如圖,拋物線y=ax2+bx+6與x軸交于點A(6,0),B(﹣1,0),與y軸交于點C.
(1)求拋物線的解析式;
(2)若點M為該拋物線對稱軸上一點,當CM+BM最小時,求點M的坐標.
(3)拋物線上是否存在點P,使△ACP為直角三角形?若存在,有幾個?寫出所有符合條件的點P的坐標;若不存在,說明理由.

【答案】(1)y=﹣x2+5x+6;(2)點M(![]() );(3)點P的坐標為(﹣2,﹣8)或(4,10)或(2+2
);(3)點P的坐標為(﹣2,﹣8)或(4,10)或(2+2![]() ,4+2
,4+2![]() )或(2﹣2
)或(2﹣2![]() ,4﹣2
,4﹣2![]() ).
).
【解析】
(1)已知C(0,6),由交點式設拋物線解析式為y=a(x+1)(x﹣6),把C點代入即可求解;
(2)先求出拋物線的對稱軸,再作出點B關于拋物線對稱軸的對稱點(即為A點),連接AC交對稱軸于點M,再求AC與對稱軸的交點可得結果;
(3)由點P在拋物線上,可先設出P點坐標,然后分別表示出PC2、PA2 、AC2,再按照∠PAC=90°、∠PCA=90°、∠APC=90°三種情況分別求解即可.
(1)當x=0時,y=ax2+bx+6=6,則C(0,6),
設拋物線的解析式為y=a(x+1)(x﹣6),
把C(0,6)代入得a1(﹣6)=6,解得a=﹣1,
∴拋物線的解析式為y=﹣(x+1)(x﹣6),即y=﹣x2+5x+6;
(2)∵拋物線的對稱軸是直線x=![]() ,直線AC的解析式為y=-x+6,點B關于對稱軸直線x=
,直線AC的解析式為y=-x+6,點B關于對稱軸直線x=![]() 的對稱點為點A,
的對稱點為點A,
∴連接AC,交直線x=![]() 于點M,此時點M滿足CM+BM最小,
于點M,此時點M滿足CM+BM最小,
當x=![]() 時,y=
時,y=![]() ,∴點M(
,∴點M(![]() )
)
(3)設P點坐標為(x,﹣x2+5x+6),存在4個點P,使△ACP為直角三角形.
PC2=x2+(﹣x2+5x)2,PA2=(x﹣6)2+(﹣x2+5x+6)2,AC2=62+62=72,
當∠PAC=90°,∵PA2+AC2=PC2,
∴(x﹣6)2+(﹣x2+5x+6)2+72=x2+(﹣x2+5x)2,
整理得x2﹣4x﹣12=0,解得x1=6(舍去),x2=﹣2,此時P點坐標為(﹣2,﹣8);
當∠PCA=90°,∵PC2+AC2=PA2,
72+x2+(﹣x2+5x)2=(x﹣6)2+(﹣x2+5x+6)2,
整理得x2﹣4x=0,解得x1=0(舍去),x2=4,此時P點坐標為(4,10);
當∠APC=90°,∵PA2+AC2=PC2,
∴(x﹣6)2+(﹣x2+5x+6)2+x2+(﹣x2+5x)2=72,
整理得x3﹣10x2+20x+24=0,
x3﹣10x2+24x﹣4x+24=0,
x(x2﹣10x+24)﹣4(x﹣6)=0,
x(x﹣4)(x﹣6)﹣4(x﹣6)=0,
(x﹣6)(x2﹣4x﹣4)=0,
而x﹣6≠0,
所以x2﹣4x﹣4=0,解得x1=2+2![]() ,x2=2﹣2
,x2=2﹣2![]() ,此時P點坐標為(2+2
,此時P點坐標為(2+2![]() ,4+2
,4+2![]() )或(2﹣2
)或(2﹣2![]() ,4﹣2
,4﹣2![]() );
);
綜上所述,符合條件的點P的坐標為(﹣2,﹣8)或(4,10)或(2+2![]() ,4+2
,4+2![]() )或(2﹣2
)或(2﹣2![]() ,4﹣2
,4﹣2![]() ).
).


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖l,在四邊形ABCD中.∠DAB被對角線AC平分,且AC2=AB·AD,我們稱該四邊形為“可分四邊形”∠DAB稱為“可分角”.

(1)如圖2,四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,求證:△DAC∽△CAB.
(2)如圖2,四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,如果∠DCB=∠DAB 則∠DAB = .
(3)現有四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,且AC=4.BC=2.∠D=90°,則AD= .
查看答案和解析>>
科目:初中數學 來源: 題型:
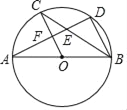
【題目】如圖,AB是⊙O的直徑,C、D是⊙O上的點,且OC∥BD,AD分別與BC、OC相較于點E、F,則下列結論:①AD⊥BD;②∠AOC=∠AEC; ③BC平分∠ABD;④△CEF≌△BED.其中一定成立的是_____(把你認為正確結論的序號都填上).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列5個結論:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的實數).其中正確結論的有( )

A. ①②③ B. ①③④ C. ③④⑤ D. ②③⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請閱讀下列材料:已知方程x2+x﹣3=0,求一個一元二次方程,使它的根分別是已知方程根的2倍.
解:設所求方程的根為y,則y=2x.所以x=![]() .
.
把x=![]() 代入已知方程,得(
代入已知方程,得(![]() )2+
)2+![]() ﹣3=0,化簡,得y2+2y﹣12=0.
﹣3=0,化簡,得y2+2y﹣12=0.
故所求方程為y2+2y﹣12=0.
這種利用方程根的代換求新方程的方法,我們稱為“換根法”.
問題:已知方程x2+x﹣1=0,求一個一元二次方程,使它的根分別是已知方程根的3倍.
查看答案和解析>>
科目:初中數學 來源: 題型:
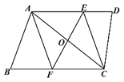
【題目】如圖,在四邊形ABCD中,AD∥BC,點O是對角線AC的中點,過點O作AC的垂線,分別交AD、BC于點E、F,連接AF、CE.試判斷四邊形AECF的形狀,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
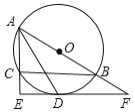
【題目】如圖,![]() 是
是![]() ABC的外接圓,AB為直徑,∠BAC的平分線交
ABC的外接圓,AB為直徑,∠BAC的平分線交![]() 于點D,過點D作DE
于點D,過點D作DE![]() AC分別交AC、AB的延長線于點E、F.
AC分別交AC、AB的延長線于點E、F.
(1)求證:EF是![]() 的切線;
的切線;
(2)若AC=4,CE=2,求![]() 的長度.(結果保留
的長度.(結果保留![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com