
 .
.
科目:初中數學 來源: 題型:閱讀理解
| 1 |
| x |
| 1 |
| x |
|
|
|
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
| 點的個數 | 可連成直線的條數 |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| … | |
| n |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
| 點的個數 | 可連成直線條數 | ||
| 2 | l=S2=
| ||
| 3 | 3=S3=
| ||
| 4 | 6=S4=
| ||
| 5 | 10=S5=
| ||
| … | … | ||
| n | Sn=
|
| 點的個數 | 可連成三角形個數 |
| 3 | |
| 4 | |
| 5 | |
| … | … |
| n |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
| n(n-1) |
| 2 |
| 點的個數 | 可連成的三角形的個數 | ||||
| 3 | 1 1 | ||||
| 4 | 4 4 | ||||
| 5 | 10 10 | ||||
| … | … | ||||
| n |
|
| n(n-1)(n-2) |
| 6 |
| n(n-1)(n-2) |
| 6 |
查看答案和解析>>
科目:初中數學 來源:2009年福建省福州市平潭縣城關中學數學模擬考試卷(解析版) 題型:解答題
 ?
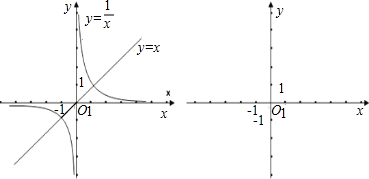
? 則在同一直角坐標系中畫出這兩個函數的草圖.
則在同一直角坐標系中畫出這兩個函數的草圖. ,解得
,解得 或
或 ∴兩個圖象的交點為(1,1)和(-1,-1)
∴兩個圖象的交點為(1,1)和(-1,-1) (1)上述解題過程用的數學思想方法是______;
(1)上述解題過程用的數學思想方法是______; 時,x的取值范圍是______;
時,x的取值范圍是______; .(要求畫出草圖)
.(要求畫出草圖)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com