
 如圖,已知⊙O上A、B、C三點,∠BAC=30°,D是OB延長線上的點,∠BDC=30°,⊙O半徑為
如圖,已知⊙O上A、B、C三點,∠BAC=30°,D是OB延長線上的點,∠BDC=30°,⊙O半徑為 .
.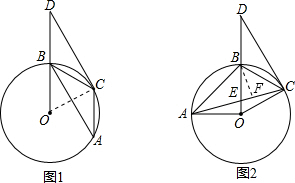 ,
,
 ,CD=
,CD= OC=
OC= ,
, ,
, +
+ );
); ∠AOB=45°,∠ABO=45°,
∠AOB=45°,∠ABO=45°, OA=2,
OA=2, AB=
AB= ×2=1,AF=
×2=1,AF= BF=
BF= ,
, +1,
+1, +1)2:22=
+1)2:22=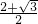 .
. ,根據含30°的直角三角形三邊的關系得到OD=2OC=2
,根據含30°的直角三角形三邊的關系得到OD=2OC=2 ,CD=
,CD= OC=
OC= ,則DB=OD-OB=
,則DB=OD-OB= ,利用平行四邊形ABDC的周長=2(DB+DC)計算即可;
,利用平行四邊形ABDC的周長=2(DB+DC)計算即可; ∠AOB=45°,∠ABO=45°,根據等腰直角三角形的性質得到AB=
∠AOB=45°,∠ABO=45°,根據等腰直角三角形的性質得到AB= OA=2,而∠CAB=∠BAE,∠ACB=∠ABO,根據相似三角形的判定得到
OA=2,而∠CAB=∠BAE,∠ACB=∠ABO,根據相似三角形的判定得到 AB=
AB= ×2=1,AF=
×2=1,AF= BF=
BF= ,
, +1,計算S△ABC:S△AEB=AC2:AB2,=(
+1,計算S△ABC:S△AEB=AC2:AB2,=( +1)2:22即可.
+1)2:22即可.

 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中數學 來源: 題型:
 (2010•北海)如圖,已知⊙O上A、B、C三點,∠BAC=30°,D是OB延長線上的點,∠BDC=30°,⊙O半徑為
(2010•北海)如圖,已知⊙O上A、B、C三點,∠BAC=30°,D是OB延長線上的點,∠BDC=30°,⊙O半徑為| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
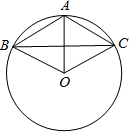 如圖,已知⊙O上的三點A、B、C,且AB=AC=6cm,BC=10cm
如圖,已知⊙O上的三點A、B、C,且AB=AC=6cm,BC=10cm查看答案和解析>>
科目:初中數學 來源: 題型:
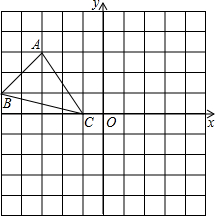 如圖,已知網格上最小的正方形的邊長為1.
如圖,已知網格上最小的正方形的邊長為1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com