【題目】a
b是新規定的一種運算法則：ab=a2+ab，例如3（﹣2）=32+3×（﹣2）=3．
（1）求（﹣3）5的值；
（2）若（﹣2）x=6，求x的值；
（3）若3（2x）=﹣4+x，求x的值．
閱讀快車系列答案科目：初中數學 來源： 題型：
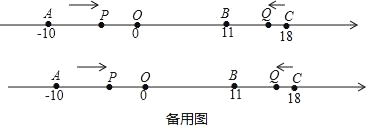
【題目】如圖，在數軸上，點A表示﹣10，點B表示11，點C表示18．動點P從點A出發，沿數軸正方向以每秒2個單位的速度勻速運動；同時，動點Q從點C出發，沿數軸負方向以每秒1個單位的速度勻速運動．設運動時間為t秒．
（1）當t為何值時，P、Q兩點相遇？相遇點M所對應的數是多少？
（2）在點Q出發后到達點B之前，求t為何值時，點P到點O的距離與點Q到點B的距離相等；
（3）在點P向右運動的過程中，N是AP的中點，在點P到達點C之前，求2CN﹣PC的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某班將買一些乒乓球和乒乓球拍，現了解情況如下：甲、乙兩家商店出售兩種同樣品牌的乒乓球和乒乓球拍．乒乓球拍每副定價30元，乒乓球每盒定價5元，經洽談后，甲店每買一副球拍贈一盒乒乓球，乙店全部按定價的9折優惠．該班需球拍5副，乒乓球若干盒（不小于5盒）．請解答下列問題：
（1）如果購買乒乓球
（
不小于5）盒，則在甲店購買需付款 元，在乙店購買需付款 元。（用
的代數式表示）
（2）當購買乒乓球多少盒時，在兩店購買付款一樣？
（3）如果給你450元，讓你選擇一家商店去辦這件事，你打算去哪家商店購買？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為減少環境污染，自2008年6月1日起，全國的商品零售場所開始實行“塑料購物袋有償使用制度”（以下簡稱“限塑令”）．某班同學于6月上旬的一天，在某超市門口采用問卷調查的方式，隨機調查了“限塑令”實施前后，顧客在該超市用購物袋的情況，以下是根據100位顧客的100份有效答卷畫出的統計圖表的一部分：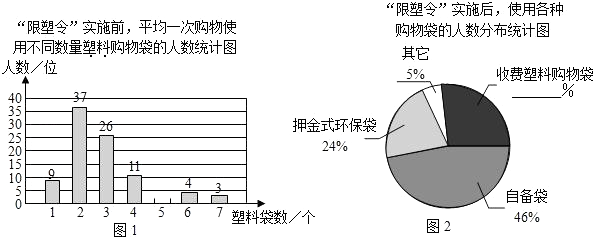 
“限塑令”實施后，塑料購物袋使用后的處理方式統計表：
處理方式 | 直接丟棄 | 直接做垃圾袋 | 再次購物使用 | 其它 |
選該項的人數占 | 5% | 35% | 49% | 11% |
請你根據以上信息解答下列問題：
（1）補全圖1，“限塑令”實施前，如果每天約有2 000人次到該超市購物．根據這100位顧客平均一次購物使用塑料購物袋的平均數，估計這個超市每天需要為顧客提供多少個塑料購物袋？
（2）補全圖2，并根據統計圖和統計表說明，購物時怎樣選用購物袋，塑料購物袋使用后怎樣處理，能對環境保護帶來積極的影響．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】要在一塊長52m，寬48m的矩形綠地上，修建同樣寬的兩條互相垂直的甬路．下面分別是小亮和小穎的設計方案．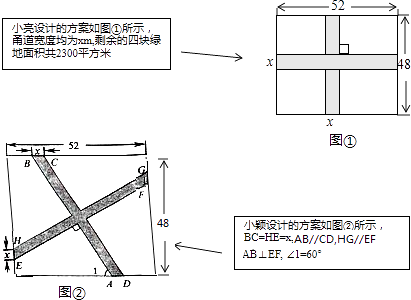 
（1）求小亮設計方案中甬路的寬度x；
（2）求小穎設計方案中四塊綠地的總面積（友情提示：小穎設計方案中的x與小亮設計方案中的x取值相同）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某批彩色彈力球的質量檢驗結果如下表：
抽取的彩色彈力球數n | 500 | 1000 | 1500 | 2000 | 2500 |
優等品頻數m | 471 | 946 | 1426 | 1898 | 2370 |
優等品頻率 | 0.942 | 0.946 | 0.951 | 0.949 | 0.948 |
（1）請在圖中完成這批彩色彈力球“優等品”頻率的折線統計圖
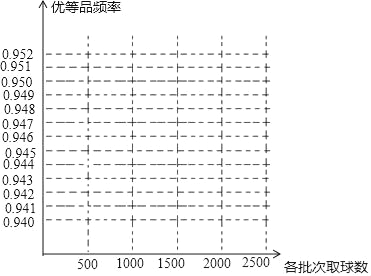
（2）這批彩色彈力球“優等品”概率的估計值大約是多少？（精確到0.01）
（3）從這批彩色彈力球中選擇5個黃球、13個黑球、22個紅球，它們除了顏色外都相同，將它們放入一個不透明的袋子中，求從袋子中摸出一個球是黃球的概率．
（4）現從第（3）問所說的袋子中取出若干個黑球，并放入相同數量的黃球，攪拌均勻，使從袋子中摸出一個黃球的概率為
，求取出了多少個黑球？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形OABC的兩邊OA、OC在坐標軸上，且OC=2OA，M、N分別為OA、OC的中點，BM與AN交于點E，若四邊形EMON的面積為2，則經過點B的雙曲線的解析式為（ ）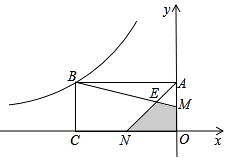 
A.y=﹣ 
B.y=﹣ 
C.y=﹣ 
D.y=﹣ 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，∠B=∠D=60°，∠BAC=∠ACD=90°，點E為邊AB上一點，AB=3AE=3cm，動點P從B點出發，以1cm/s的速度沿BC→CD→DA運動至A點停止，設運動時間為t秒．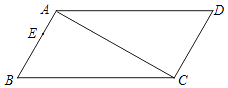
（1）求證四邊形ABCD是平行四邊形；
（2）當△BEP為等腰三角形時，求t2﹣31t的值；
（3）當t=4時，把△ABP沿直線AP翻折，得到△AFP，求△AFP與ABCD重疊部分的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平行四邊形ABCD中，E、F分別在AD、BC邊上，且AE=CF．
求證：（1）△ABE≌△CDF；
（2）四邊形BFDE是平行四邊形．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
