
 EH×AG+
EH×AG+ EH×DT=
EH×DT= EH(AG+DT)=
EH(AG+DT)= (-m2+3m+4-m-1)×5=-
(-m2+3m+4-m-1)×5=- (m-1)2+10
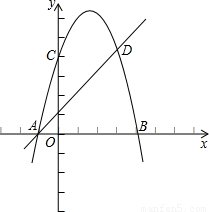
(m-1)2+10 <0,∴S△AED有最大值.當m=1時,最大值為10,此時點E的坐標為(1,10).
<0,∴S△AED有最大值.當m=1時,最大值為10,此時點E的坐標為(1,10).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
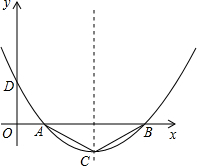 如圖,二次函數的圖象經過點D(0,
如圖,二次函數的圖象經過點D(0,| 7 |
| 9 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,二次函數y=ax2+bx+c的圖象與x軸交于B、C兩點,與y軸交于點A(0,-3),∠ABC=45°,∠ACB=60°,求這個二次函數解析式.
如圖,二次函數y=ax2+bx+c的圖象與x軸交于B、C兩點,與y軸交于點A(0,-3),∠ABC=45°,∠ACB=60°,求這個二次函數解析式.查看答案和解析>>
科目:初中數學 來源: 題型:
 某公司推出了一種高效環保型洗滌用品,年初上市后,公司經歷了從虧損到盈利的過程,如圖的二次函數圖象(部分)刻畫了該公司年初以來累積利潤s(萬元)與時間t(月)之間的關系(即前t個月的利潤總和s與t之間的關系).根據圖象提供的信息,解答下列問題:
某公司推出了一種高效環保型洗滌用品,年初上市后,公司經歷了從虧損到盈利的過程,如圖的二次函數圖象(部分)刻畫了該公司年初以來累積利潤s(萬元)與時間t(月)之間的關系(即前t個月的利潤總和s與t之間的關系).根據圖象提供的信息,解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,二次函數y=ax2+bx+c的圖象與x軸相交于兩個點,根據圖象回答:(1)b
如圖,二次函數y=ax2+bx+c的圖象與x軸相交于兩個點,根據圖象回答:(1)b查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com