
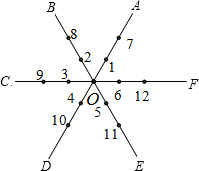
 如圖所示,平面內有公共端點的六條射線OA,OB,OC,OD,OE,OF,從射線OA開始按逆時針方向依次在射線上寫出數字1,2,3,4,5,6,7,….
如圖所示,平面內有公共端點的六條射線OA,OB,OC,OD,OE,OF,從射線OA開始按逆時針方向依次在射線上寫出數字1,2,3,4,5,6,7,….

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中數學 來源: 題型:
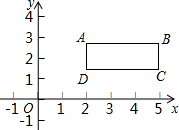 如圖所示,平面內有四個點,它們的坐標分別是A(2,2
如圖所示,平面內有四個點,它們的坐標分別是A(2,2| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖所示,平面內有公共端點的六條射線OA,OB,OC,OD,OE,OF,從射線OA開始按逆時針方向依次在射線上寫出數字1,2,3,4,5,6,7,….
如圖所示,平面內有公共端點的六條射線OA,OB,OC,OD,OE,OF,從射線OA開始按逆時針方向依次在射線上寫出數字1,2,3,4,5,6,7,….查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖所示,平面內有四個點A,B,C,D,按下列語句畫出圖形.
如圖所示,平面內有四個點A,B,C,D,按下列語句畫出圖形.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
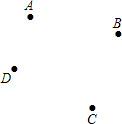 如圖所示,平面內有四個點A,B,C,D,按下列語句畫出圖形.
如圖所示,平面內有四個點A,B,C,D,按下列語句畫出圖形.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com