
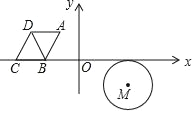
【題目】如圖,⊙M與菱形ABCD在平面直角坐標系中,點M的坐標為(3,﹣1),點A的坐標為(﹣2,![]() ),點B的坐標為(﹣3,0),點C在x軸上,且點D在點A的左側.
),點B的坐標為(﹣3,0),點C在x軸上,且點D在點A的左側.
(1)求菱形ABCD的周長;
(2)若⊙M沿x軸向右以每秒2個單位長度的速度平移,同時菱形ABCD沿x軸向右以每秒3個單位長度的速度平移,設菱形移動的時間為t(秒),當⊙M與BC相切,且切點為BC的中點時,連接BD,求:
①t的值;
②∠MBD的度數;
(3)在(2)的條件下,當點M與BD所在的直線的距離為1時,求t的值.
【答案】(1)8;(2)①7;②105°;(3)t=6﹣![]() 或6+
或6+![]() .
.
【解析】分析:(1)根據勾股定理求菱形的邊長為2,所以可得周長為8;
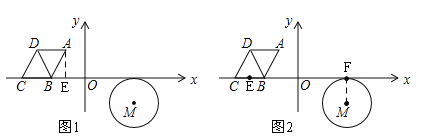
(2)①如圖2,先根據坐標求EF的長,由EE'﹣FE'=EF=7,列式得:3t﹣2t=7,可得t的值;
②先求∠EBA=60°,則∠FBA=120°,再得∠MBF=45°,相加可得:∠MBD=∠MBF+∠FBD=45°+60°=105°;
(3)分兩種情況討論:作出距離MN和ME,第一種情況:如圖5由距離為1可知:BD為⊙M的切線,由BC是⊙M的切線,得∠MBE=30°,列式為3t+![]() =2t+6,解出即可;
=2t+6,解出即可;
第二種情況:如圖6,同理可得t的值.
詳解:(1)如圖1,過A作AE⊥BC于E.
∵點A的坐標為(﹣2,![]() ),點B的坐標為(﹣3,0),∴AE=
),點B的坐標為(﹣3,0),∴AE=![]() ,BE=3﹣2=1,∴AB=
,BE=3﹣2=1,∴AB=![]() =
=![]() =2.
=2.
∵四邊形ABCD是菱形,∴AB=BC=CD=AD=2,∴菱形ABCD的周長=2×4=8;
(2)①如圖2,⊙M與x軸的切點為F,BC的中點為E.
∵M(3,﹣1),∴F(3,0).
∵BC=2,且E為BC的中點,∴E(﹣4,0),∴EF=7,即EE'﹣FE'=EF,∴3t﹣2t=7,t=7;
②由(1)可知:BE=1,AE=![]() ,
,
∴tan∠EBA=![]() =
=![]() =
=![]() ,∴∠EBA=60°,如圖4,∴∠FBA=120°.
,∴∠EBA=60°,如圖4,∴∠FBA=120°.
∵四邊形ABCD是菱形,∴∠FBD=![]() ∠FBA=
∠FBA=![]() =60°.
=60°.
∵BC是⊙M的切線,∴MF⊥BC.
∵F是BC的中點,∴BF=MF=1,∴△BFM是等腰直角三角形,
∴∠MBF=45°,∴∠MBD=∠MBF+∠FBD=45°+60°=105°;
(3)連接BM,過M作MN⊥BD,垂足為N,作ME⊥BC于E,分兩種情況:
第一種情況:如圖5.
∵四邊形ABCD是菱形,∠ABC=120°,∴∠CBD=60°,∴∠NBE=60°.
∵點M與BD所在的直線的距離為1,∴MN=1,∴BD為⊙M的切線.
∵BC是⊙M的切線,∴∠MBE=30°.
∵ME=1,∴EB=![]() ,∴3t+
,∴3t+![]() =2t+6,t=6﹣
=2t+6,t=6﹣![]() ;
;
第二種情況:如圖6.
∵四邊形ABCD是菱形,∠ABC=120°,∴∠DBC=60°,∴∠NBE=120°.
∵點M與BD所在的直線的距離為1,∴MN=1,∴BD為⊙M的切線.
∵BC是⊙M的切線,∴∠MBE=60°.
∵ME=MN=1,∴Rt△BEM中,tan60°=![]() ,EB=
,EB=![]() =
=![]() ,
,
∴3t=2t+6+![]() ,t=6+
,t=6+![]() ;
;
綜上所述:當點M與BD所在的直線的距離為1時,t=6﹣![]() 或6+
或6+![]() .
.




 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:
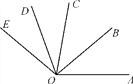
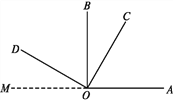
【題目】如圖,OB為∠AOC的平分線,OD是∠COE的平分線.
(1)如果∠AOB=40°,∠DOE=30°,那么∠BOD為多少度?
(2)如果∠AOE=140°,∠COD=30°,那么∠AOB為多少度?
查看答案和解析>>
科目:初中數學 來源: 題型:
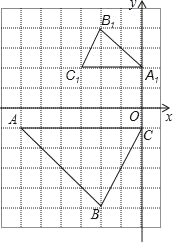
【題目】如圖,△ABC與△A1B1C1是位似圖形.
(1)在網格上建立平面直角坐標系,使得點A的坐標為(﹣6,﹣1),點C1的坐標為(﹣3,2),則點B的坐標為 ;
(2)以點A為位似中心,在網格圖中作△AB2C2,使△AB2C2和△ABC位似,且位似比為1:2;
(3)在圖上標出△ABC與△A1B1C1的位似中心P,并寫出點P的坐標為 ,計算四邊形ABCP的周長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
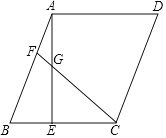
【題目】在ABCD中,AE⊥BC于點E,F為AB邊上一點,連接CF,交AE于點G,CF=CB=AE.
(1)若AB![]() ,BC
,BC![]() ,求CE的長;
,求CE的長;
(2)求證:BE=CG﹣AG.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點N(0,6),點M在x軸負半軸上,ON=3OM.A為線段MN上一點,AB⊥x軸,垂足為點B,AC⊥y軸,垂足為點C.
(1)寫出點M的坐標;
(2)求直線MN的表達式;
(3)若點A的橫坐標為-1,求矩形ABOC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,OB是∠AOC的平分線,OD是∠COE的平分線.
(1)若∠AOB=50°,∠DOE=35°,求∠BOD的度數;
(2)若∠AOE=160°,∠COD=40°,求∠AOB的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
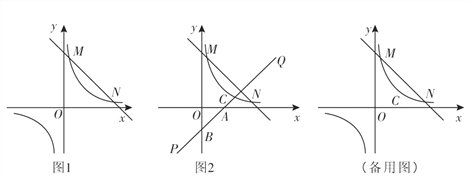
【題目】如圖1 ,一次函數![]() (k,b為常數,k≠0)的圖象與反比例函數
(k,b為常數,k≠0)的圖象與反比例函數![]() (m為常數,m≠0)的圖象相交于點M(1,4)和點N(4,n).
(m為常數,m≠0)的圖象相交于點M(1,4)和點N(4,n).
(1)填空:①反比例函數的解析式是 ; ②根據圖象寫出![]() 時自變量x的取值范圍是 ;
時自變量x的取值范圍是 ;
(2) 若將直線MN向下平移a(a>0)個單位長度后與反比例函數的圖象有且只有一個公共點,求a的值;
(3) 如圖2,函數![]() 的圖象(x>0)上有一個動點C,若先將直線MN平移使它過點C,再繞點C旋轉得到直線PQ,PQ交
的圖象(x>0)上有一個動點C,若先將直線MN平移使它過點C,再繞點C旋轉得到直線PQ,PQ交![]() 軸于點A,交
軸于點A,交![]() 軸點B,若BC=2CA, 求OA·OB的值.
軸點B,若BC=2CA, 求OA·OB的值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀解題過程,回答問題.
如圖,OC在∠AOB內,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度數.
解:過O點作射線OM,使點M,O,A在同一直線上.
因為∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,所以∠BOC=∠MOD,
所以∠AOD=180°-∠BOC=180°-30°=150°.
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() (如圖),點
(如圖),點![]() 分別在邊
分別在邊![]() 上,且四邊形
上,且四邊形![]() 是菱形
是菱形
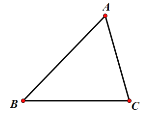
(1)請使用直尺與圓規,分別確定點![]() 的具體位置(不寫作法,保留畫圖痕跡);
的具體位置(不寫作法,保留畫圖痕跡);
(2)如果![]() ,點
,點![]() 在邊
在邊![]() 上,且滿足
上,且滿足![]() ,求四邊形
,求四邊形![]() 的面積;
的面積;
(3)當![]() 時,求
時,求![]() 的值。
的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com