
【題目】如圖,在⊙O中,AB是⊙O的直徑,AB=10, ![]() ,點E是點D關于AB的對稱點,M是AB上的一動點,下列結論:①∠BOE=60°;②∠CED=
,點E是點D關于AB的對稱點,M是AB上的一動點,下列結論:①∠BOE=60°;②∠CED=![]() ∠AOD;③DM⊥CE;④CM+DM的最小值是10,其中正確的序號是______.
∠AOD;③DM⊥CE;④CM+DM的最小值是10,其中正確的序號是______.

【答案】①④
【解析】∵![]() ,點E是點D關于AB的對稱點,
,點E是點D關于AB的對稱點,
∴![]() ,
,
∴∠DOB=∠BOE=∠COD=![]() ×180°=60°,∴①正確;
×180°=60°,∴①正確;
∠CED=![]() ∠COD=
∠COD=![]() ×60°=30°=
×60°=30°=![]() ∠DOB,∴②錯誤;
∠DOB,∴②錯誤;
∵![]() 的度數是60°,
的度數是60°,
∴![]() 的度數是120°,
的度數是120°,
∴只有當M和A重合時,∠MDE=60°,
∵∠CED=30°,
∴只有M和A重合時,DM⊥CE,∴③錯誤;
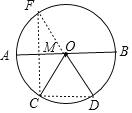
做C關于AB的對稱點F,連接CF,交AB于M,此時CM+DM的值最短,等于DF長,
連接CD,
∵![]() ,并且弧的度數都是60°,
,并且弧的度數都是60°,
∴∠D=![]() ×120°=60°,∠CFD=
×120°=60°,∠CFD=![]() ×60°=30°,
×60°=30°,
∴∠FCD=180°60°30°=90°,
∴DF是⊙O的直徑,
即DF=AB=10,
∴CM+DM的最小值是10,∴④正確;
故答案為:①④.


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,弦CD⊥AB于E,∠CDB=15°,OE=2![]() .
.
(1)求⊙O的半徑;
(2)將△OBD繞O點旋轉,使弦BD的一個端點與弦AC的一個端點重合,則弦BD與弦AC的夾角為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在大課間活動中,同學們積極參加體育鍛煉,小龍在全校隨機抽取一部分同學就“我最喜愛的體育項目”進行了一次抽樣調查,下面是他通過收集的數據繪制的兩幅不完整的統計圖,請你根據圖中提供的信息,解答以下問題:
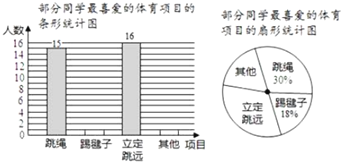
(1)小龍共抽取______名學生;
(2)補全條形統計圖;
(3)在扇形統計圖中,“其他”部分對應的圓心角的度數是_______;
(4)若全校共2100名學生,請你估算“立定跳遠”部分的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(圖①為實景側視圖,圖②為安裝示意圖),在屋頂的斜坡面上安裝太陽能熱水器:先安裝支架AB和CD(均與水平面垂直),再將集熱板安裝在AD上.為使集熱板吸熱率更高,公司規定:AD與水平線夾角為θ1,且在水平線上的射影AF為1.4 m.現已測量出屋頂斜面與水平面夾角為θ2,并已知tan θ1=1.082,tan θ2=0.412.如果安裝工人已確定支架AB高為25 cm,求支架CD的高.(結果精確到1 cm)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,AB=8cm,AD=12cm,點P在AD邊上以每秒1cm 的速度從點A向點D運動,點Q在BC邊上,以每秒4cm的速度從點C出發,在CB間往返運動,兩個點同時出發,當點P到達點D時停止(同時點Q也停止),在運動以后,以P、D、Q、B四點組成平行四邊形的次數有__次.

查看答案和解析>>
科目:初中數學 來源: 題型:
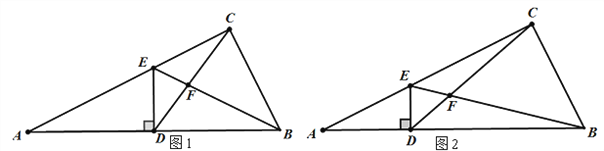
【題目】如圖1,點D為直角三角形ABC的斜邊AB上的中點,DE⊥AB交AC于E, 連EB、CD,線段CD與BF交于點F.若tanA=![]() ,則
,則![]() =_____.如圖2,點D為直角三角形ABC的斜邊AB上的一點,DE⊥AB交AC于E, 連EB、CD;線段CD與BF交于點F.若
=_____.如圖2,點D為直角三角形ABC的斜邊AB上的一點,DE⊥AB交AC于E, 連EB、CD;線段CD與BF交于點F.若![]() ,tanA=
,tanA=![]() ,則
,則![]() =____.
=____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC中,AB=AC.
(1)如圖1,如果∠BAD=30°,AD是BC上的高,AD=AE,則∠EDC=_____度;
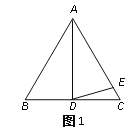
(2)如圖2,如果∠BAD=40°,AD是BC上的高,AD=AE,則∠EDC=_______度;
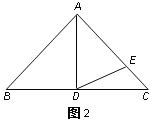
(3)思考:通過以上兩題,你發現∠BAD與∠EDC之間有什么關系?請用式子表示:____________________.
(4)如圖3,如果AD不是BC上的高,AD=AE,是否仍有上述關系?如有,請你寫出來,并說明理由.
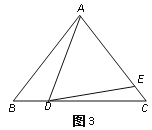
查看答案和解析>>
科目:初中數學 來源: 題型:
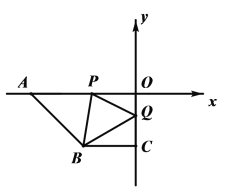
【題目】如圖,在平面直角坐標系xOy中,點A(a,0),B(c,c),C(0,c),且滿足![]() ,P點從A點出發沿x軸正方向以每秒2個單位長度的速度勻速移動,Q點從O點出發沿y軸負方向以每秒1個單位長度的速度勻速移動.
,P點從A點出發沿x軸正方向以每秒2個單位長度的速度勻速移動,Q點從O點出發沿y軸負方向以每秒1個單位長度的速度勻速移動.
(1)直接寫出點B的坐標,AO和BC位置關系是;
(2)當P、Q分別是線段AO,OC上時,連接PB,QB,使![]() ,求出點P的坐標;
,求出點P的坐標;
(3)在P、Q的運動過程中,當∠CBQ=30°時,請探究∠OPQ和∠PQB的數量關系,并說明理由.
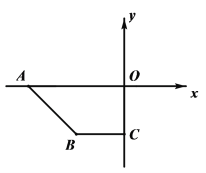
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com