
【題目】如圖,![]() 為
為![]() 的直徑,
的直徑,![]() 于點
于點 ![]() ,
,![]() 是
是![]() 上一點,且
上一點,且![]() ,延長
,延長![]() 至點
至點![]() ,連接
,連接![]() ,使
,使![]() ,延長
,延長![]() 與
與![]() 交于點
交于點![]() ,連結
,連結![]() ,
,![]() .
.
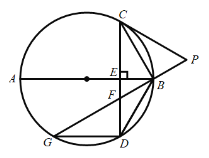
(1)連結![]() ,求證:
,求證:![]() ;
;
(2)求證:![]() 是
是![]() 的切線;
的切線;
(3)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)見解析;(2)見解析;(3)![]()
【解析】
(1)證得![]() ,根據AAS可證得△BCD≌△DGB,從而結論得證;
,根據AAS可證得△BCD≌△DGB,從而結論得證;
(2)連接OC,由于![]() ,
,![]() ,從而可得
,從而可得![]() ,又因為PC=PF,從而可知
,又因為PC=PF,從而可知![]() ,由于AB⊥CD,∠COB+∠OCE=90°,所以
,由于AB⊥CD,∠COB+∠OCE=90°,所以![]() ,從而得證;
,從而得證;
(3)連接![]() ,證得
,證得![]() ,所以tanG=tan∠BCD=
,所以tanG=tan∠BCD=![]() ,設
,設![]() ,則
,則![]() ,
,![]() ,從而可求出BE,CE的長度,再由勾股定理可知BC的長度,證明
,從而可求出BE,CE的長度,再由勾股定理可知BC的長度,證明![]() ,得出
,得出![]() ,從而可求出FD.
,從而可求出FD.
解:(1)證明:∵![]() ,∴
,∴![]() ,
,
∵![]() ∴
∴![]()
∵![]() ∴
∴![]()
∴![]()
(2)證明:連接![]() .
.
∵![]() ∴
∴![]()
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 是圓
是圓![]() 的切線.
的切線.
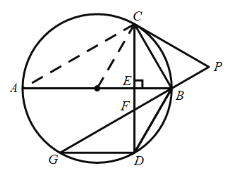
(3)連接![]() ,∵直徑
,∵直徑![]() 弦
弦![]() 于
于![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]()
設![]() ,則
,則![]() ,
,![]()
∵![]()
∴![]()
解得![]() ,
,
∴![]() ,
,![]()
∴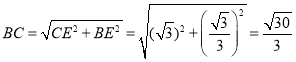 ,
,![]()
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∵![]()
∴![]() ,
,
![]()
即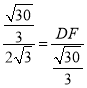 ,
,
∴![]()


科目:初中數學 來源: 題型:
【題目】現有![]() ,
,![]() 兩個不透明的袋子,分別裝有3個除顏色外完全相同的小球.其中,
兩個不透明的袋子,分別裝有3個除顏色外完全相同的小球.其中,![]() 袋裝有1個白球,2個紅球;
袋裝有1個白球,2個紅球;![]() 袋裝有1個紅球,2個白球.
袋裝有1個紅球,2個白球.
(1)將![]() 袋搖勻,然后從
袋搖勻,然后從![]() 袋中隨機摸出一個球,則摸出的小球是紅球的概率為______;
袋中隨機摸出一個球,則摸出的小球是紅球的概率為______;
(2)小王和小周商定了一個游戲規則:從搖勻后的![]() ,
,![]() 兩袋中各隨機摸出一個球,摸出的這兩個球,若顏色相同,則小王獲勝;若顏色不同,則小周獲勝.請利用概率說明這個游戲規則是否公平.
兩袋中各隨機摸出一個球,摸出的這兩個球,若顏色相同,則小王獲勝;若顏色不同,則小周獲勝.請利用概率說明這個游戲規則是否公平.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市一研究機構為了了解![]() 歲年齡段市民對創建文明城市的關注程度,隨機選取了
歲年齡段市民對創建文明城市的關注程度,隨機選取了![]() 名年齡在該范圍內的市民進行了調查,并將收集到的數據制成了尚不完整的頻數分布表、頻數分布直方圖和扇形統計圖,如下所示:
名年齡在該范圍內的市民進行了調查,并將收集到的數據制成了尚不完整的頻數分布表、頻數分布直方圖和扇形統計圖,如下所示:
組別 | 年齡段 | 頻數(人數) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
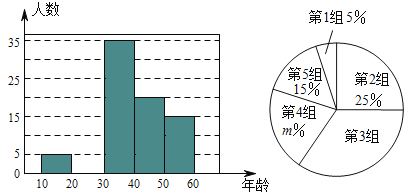
(1)請直接寫出![]() ,第
,第![]() 組人數在扇形統計圖中所對應的圓心角是 度;
組人數在扇形統計圖中所對應的圓心角是 度;
(2)請補全上面的頻數分布直方圖:
(3)假設該市現有![]() 歲的市民
歲的市民![]() 萬人,問
萬人,問![]() 歲年齡段的關注創建文明城市的人數約有多少?
歲年齡段的關注創建文明城市的人數約有多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】第5代移動通信技術簡稱5G,某地已開通5G業務,經測試5G下載速度是4G下載速度的15倍,小明和小強分別用5G與4G下載一部600兆的公益片,小明比小強所用的時間快140秒,求該地4G與5G的下載速度分別是每秒多少兆?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】PM2.5是指大氣中直徑小于或等于2.5μm(0.0000025m)的顆粒物,含有大量有毒、有害物質,也稱可入肺顆粒物.將0.0000025用科學記數法表示為
A.25×10﹣7B.2.5×10﹣6C.0.25×10﹣5D.2.5×106
查看答案和解析>>
科目:初中數學 來源: 題型:
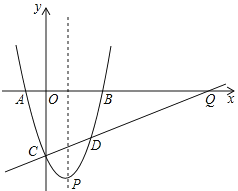
【題目】如圖,已知拋物線與![]() 軸交于
軸交于![]() ,
,![]() 點,與
點,與![]() 軸交于點
軸交于點![]() ,拋物線的頂點為
,拋物線的頂點為![]() ,連接
,連接![]() .
.
(1)求此拋物線的表達式;
(2)在拋物線上找一點![]() ,使得
,使得![]() 與
與![]() 垂直,且直線
垂直,且直線![]() 與
與![]() 軸交于點
軸交于點![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)拋物線對稱軸上是否存在一點![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 點坐標;若不存在,請說明理由.
點坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
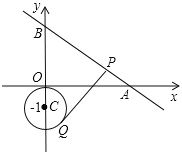
【題目】如圖,直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ;點
;點![]() 是以
是以![]() 為圓心,1為半徑的圓上一動點,過Q點的切線交線段AB于點P,當線段PQ取最小值時,P點的坐標是__________.
為圓心,1為半徑的圓上一動點,過Q點的切線交線段AB于點P,當線段PQ取最小值時,P點的坐標是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com