
為了預防流感,某學校對教室采用藥薰消毒法進行消毒,已知藥物燃燒時,室內每立方米空氣中的含藥量y(毫克)與時間x(分鐘)成正比例,藥物燃燒后,y與x成反比例(如圖),現測藥物8分鐘燃畢,此時空氣中每立方米含藥量為6毫克,請根據題中所提供的信息,回答下列問題
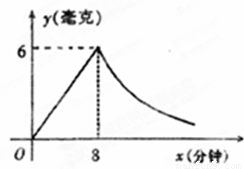
(1)藥物燃燒時,y關于x的函數關系式為 ,自變量x的取值范圍是 ;藥物燃燒完后,y與x的函數關系式為
(2)研究表明,當空氣中的每立方米的含藥量低于1.6毫克時學生方可進教室,那么從消毒開始,至少需要經過幾分鐘后,學生才能回到教室.
(3)研究表明,當空氣中每立方米的含藥量不低于3毫克且持續時間不低于10分鐘時,才能有效地殺滅空氣中的病菌,那么此次消毒是否有效?為什么?
(1)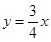 ,0≤x≤8,
,0≤x≤8, ;
;
(2)從消毒開始,至少需要經過30分鐘后,學生才能回到教室;
(3)此次消毒是無效的,理由見解析.
【解析】
試題分析:(1)由于在藥物燃燒階段,y與x成正比例,因此設函數解析式為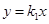 (k1≠0),然后由(8,6)在函數圖象上,利用待定系數法即可求得藥物燃燒時y與x的函數解析式;由于在藥物燃燒階段后,y與x成反比例,因此設函數解析式為
(k1≠0),然后由(8,6)在函數圖象上,利用待定系數法即可求得藥物燃燒時y與x的函數解析式;由于在藥物燃燒階段后,y與x成反比例,因此設函數解析式為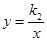 (k2≠0),然后由(8,6)在函數圖象上,利用待定系數法即可求得藥物燃燒階段后y與x的函數解析式;
(k2≠0),然后由(8,6)在函數圖象上,利用待定系數法即可求得藥物燃燒階段后y與x的函數解析式;
(2)當空氣中的每立方米的含藥量低于1.6毫克時學生方可進教室,把y=1.6代入 ,即可求得y的值,則可求得答案;
,即可求得y的值,則可求得答案;
(3)把y=3代入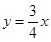 中得x=4, 把y=3代入
中得x=4, 把y=3代入 中得x=16,(8-4)+(16-8)=12>10得知此次消毒是無效的.
中得x=16,(8-4)+(16-8)=12>10得知此次消毒是無效的.
試題解析:(1)∵設正比例函數解析式為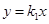 (k1≠0),函數的圖象經過點P(8,6)
(k1≠0),函數的圖象經過點P(8,6)
∴正比例函數的解析式為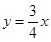 .自變量x的取值范圍是0≤x≤8;
.自變量x的取值范圍是0≤x≤8;
∵設反比例函數解析式為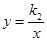 (k2≠0),函數的圖象經過點P(8,6),
(k2≠0),函數的圖象經過點P(8,6),
∴反比例函數的解析式為 .
自變量x的取值范圍是x≥4;
.
自變量x的取值范圍是x≥4;
(2)把y=1.6代入 中得x=30,
中得x=30,
∴從消毒開始,至少需要經過30分鐘后,學生才能回到教室;
(3)把y=3代入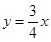 中得x=4,
中得x=4,
把y=3代入 中得x=16,
中得x=16,
(8-4)+(16-8)=12>10,
∴此次消毒是無效的.
考點:反比例函數的應用.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:
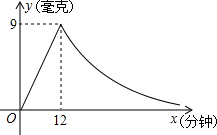 教室,那么從藥物釋放開始,至少需要經過多少小時后,學生才能進入教室?
教室,那么從藥物釋放開始,至少需要經過多少小時后,學生才能進入教室?查看答案和解析>>
科目:初中數學 來源: 題型:
| a | t |
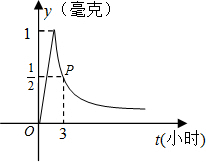 教室,那么從藥物釋放開始,至少需要經過多少小時后,學生才能進入教室?
教室,那么從藥物釋放開始,至少需要經過多少小時后,學生才能進入教室?查看答案和解析>>
科目:初中數學 來源: 題型:
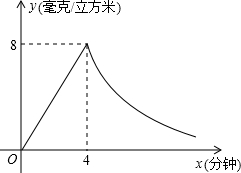 燃畢,此時室內空氣中每立方米含藥量為8毫克.請根據題中所提供的信息,解答下列問題:
燃畢,此時室內空氣中每立方米含藥量為8毫克.請根據題中所提供的信息,解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:
 為了預防流感,某學校在休息天用藥熏消毒法對教室進行消毒,已知藥物釋放過程中,室內每立方米空氣中的含藥量y(毫克)與時間t(小時)成正比;藥物釋放完畢后,y與t的函數關系式為y=
為了預防流感,某學校在休息天用藥熏消毒法對教室進行消毒,已知藥物釋放過程中,室內每立方米空氣中的含藥量y(毫克)與時間t(小時)成正比;藥物釋放完畢后,y與t的函數關系式為y=| a | t |
查看答案和解析>>
科目:初中數學 來源: 題型:
 為了預防流感,某學校在休息天用藥熏消毒法對教室進行消毒.已知藥物釋放過程中,室內每立方米空氣中的含藥量y(毫克)與時間t(小時)成正比;藥物釋放完畢后,y與t的函數關系式為y=
為了預防流感,某學校在休息天用藥熏消毒法對教室進行消毒.已知藥物釋放過程中,室內每立方米空氣中的含藥量y(毫克)與時間t(小時)成正比;藥物釋放完畢后,y與t的函數關系式為y=| a | t |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com