Question

3．將一副三角板中的兩塊直角三角尺的直角頂點O按如圖方式疊放在一起．

（1）如圖（1）若∠BOD=35°，則∠AOC=145°；若∠AOC=135°，則∠BOD=45°；
（2）如圖（2）若∠AOC=140°，則∠BOD=40°；
（3）猜想∠AOC與∠BOD的大小關系，并結合圖（1）說明理由．
（4）三角尺AOB不動，將三角尺COD的OD邊與OA邊重合，然后繞點O按順時針或逆時針方向任意轉動一個角度，當∠AOD（0°＜∠AOD＜90°）等于多少度時，這兩塊三角尺各有一條邊互相垂直，直接寫出∠AOD角度所有可能的值，不用說明理由．

Answer 1

分析 （1）由于是兩直角三角形板重疊，根據∠AOC=∠AOB+∠COD-∠BOD可分別計算出∠AOC、∠BOD的度數；
（2）根據∠BOD=360°-∠AOC-∠AOB-∠COD計算可得；
（3）由∠AOD+∠BOD+∠BOD+∠BOC=180°且∠AOD+∠BOD+∠BOC=∠AOC可知兩角互補；
（4）分別利用OD⊥AB、CD⊥OB、CD⊥AB、OC⊥AB分別求出即可．

解答 解：（1）若∠BOD=35°，∵∠AOB=∠COD=90°，
∴∠AOC=∠AOB+∠COD-∠BOD=90°+90°-35°=145°，
若∠AOC=135°，
則∠BOD=∠AOB+∠COD-∠AOC=90°+90°-135°=45°；

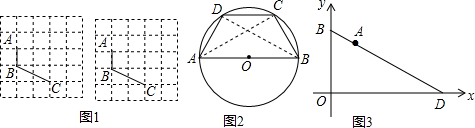
（2）如圖2，若∠AOC=140°，
則∠BOD=360°-∠AOC-∠AOB-∠COD=40°；

（3）∠AOC與∠BOD互補．
∵∠AOD+∠BOD+∠BOD+∠BOC=180°．
∵∠AOD+∠BOD+∠BOC=∠AOC，
∴∠AOC+∠BOD=180°，
即∠AOC與∠BOD互補．

（4）OD⊥AB時，∠AOD=30°，
CD⊥OB時，∠AOD=45°，
CD⊥AB時，∠AOD=75°，
OC⊥AB時，∠AOD=60°，
即∠AOD角度所有可能的值為：30°、45°、60°、75°；
故答案為：（1）145°，45°；（2）40°．

點評 本題題主要考查了互補、互余的定義等知識，解決本題的關鍵是理解重疊的部分實質是兩個角的重疊．