
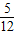 ?若存在,求出此時BH的長度;若不存在,說明理由.
?若存在,求出此時BH的長度;若不存在,說明理由. x2-3x+9,根據△GKH的面積恰好等于△ABC面積的
x2-3x+9,根據△GKH的面積恰好等于△ABC面積的 ,代入得出方程
,代入得出方程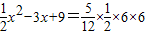 ,求出即可.
,求出即可.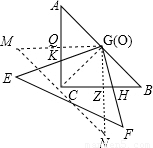 解:(1)BH與CK的數量關系:BH=CK,理由是:
解:(1)BH與CK的數量關系:BH=CK,理由是: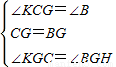 ,
,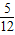 的位置.
的位置.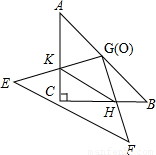
 CH×CK=3x-
CH×CK=3x- x2,
x2, x2)=
x2)= x2-3x+9,
x2-3x+9,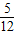 ,
, x2-3x+9=
x2-3x+9=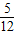 ×
× ×6×6,
×6×6,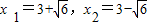 (經檢驗,均符合題意).
(經檢驗,均符合題意). 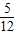 的位置,此時x的值為
的位置,此時x的值為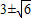 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
| 5 | 12 |
查看答案和解析>>
科目:初中數學 來源: 題型:
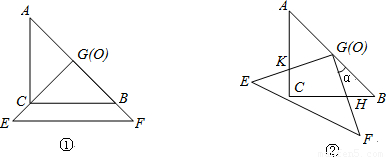
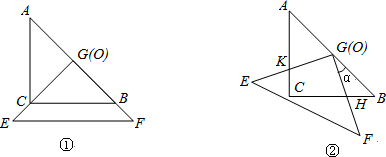
(本題8分)把兩個直角邊長均為6的等腰直角三角板ABC和EFG疊放在一起(如圖①),使三角板EFG的直角頂點G與三角板ABC的斜邊中點O重合.現將三角板EFG繞O點順時針旋轉(旋轉角α滿足條件:0°<α<90°),四邊形CHGK是旋轉過程中兩三角板的重疊部分(如圖②).

1.(1) 探究:在上述旋轉過程中,BH與CK的數量關系以及四邊形CHGK的面積的變化情況(直接寫出探究的結果,不必寫探究及推理過程);
2.(2) 利用(1)中你得到的結論,解決下面問題:連接HK,在上述旋轉過程中,是否存在某一位置,使△GKH的面積恰好等于△ABC面積的![]() ?若存在,求出此時BH的長度;若不存在,說明理由.
?若存在,求出此時BH的長度;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
 程中兩三角板的重疊部分(如圖②).
程中兩三角板的重疊部分(如圖②).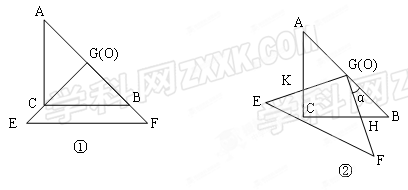
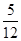 ?若存在,求出此時BH的長度;若不存在,說明理由.
?若存在,求出此時BH的長度;若不存在,說明理由.查看答案和解析>>
科目:初中數學 來源:2012屆北京市101中學九年級第一次月考數學卷 題型:解答題
(本題8分)把兩個直角邊長均為6的等腰直角三角板ABC和EFG疊放在一起(如圖①),使三角板EFG的直角頂點G與三角板ABC的斜邊中點O重合.現將三角板EFG繞O點順時針旋轉(旋轉角α滿足條件:0°<α<90°),四邊形CHGK是旋轉過 程中兩三角板的重疊部分(如圖②).
程中兩三角板的重疊部分(如圖②).
【小題1】(1) 探究:在上述旋轉過程中,BH與CK的數量關系以及四邊形CHGK的面積的變化情況(直接寫出探究的結果,不必寫探究及推理過程);
【小題2】(2) 利用(1)中你得到的結論,解決下面問題:連接HK,在上述旋轉過程中,是否存在某一位置,使△GKH的面積恰好等于△ABC面積的 ?若存在,求出此時BH的長度;若不存在,說明理由.
?若存在,求出此時BH的長度;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源:2011-2012學年北京市九年級第一次月考數學卷 題型:解答題
(本題8分)把兩個直角邊長均為6的等腰直角三角板ABC和EFG疊放在一起(如圖①),使三角板EFG的直角頂點G與三角板ABC的斜邊中點O重合.現將三角板EFG繞O點順時針旋轉(旋轉角α滿足條件:0°<α<90°),四邊形CHGK是旋轉過程中兩三角板的重疊部分(如圖②).

1.(1) 探究:在上述旋轉過程中,BH與CK的數量關系以及四邊形CHGK的面積的變化情況(直接寫出探究的結果,不必寫探究及推理過程);
2.(2) 利用(1)中你得到的結論,解決下面問題:連接HK,在上述旋轉過程中,是否存在某一位置,使△GKH的面積恰好等于△ABC面積的 ?若存在,求出此時BH的長度;若不存在,說明理由.
?若存在,求出此時BH的長度;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com