
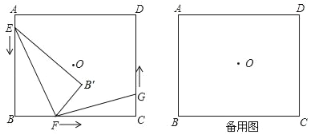
【題目】如圖,點O為矩形ABCD的對稱中心,AB=5cm,BC=6cm,點E.F.G分別從A.B.C三點同時出發,沿矩形的邊按逆時針方向勻速運動,點E的運動速度為1cm/s,點F的運動速度為3cm/s,點G的運動速度為1.5cm/s,當點F到達點C(即點F與點C重合)時,三個點隨之停止運動.在運動過程中,△EBF關于直線EF的對稱圖形是△EB′F.設點E.F.G運動的時間為t(單位:s).
(1)當t等于多少s時,四邊形EBFB′為正方形;
(2)若以點E、B、F為頂點的三角形與以點F,C,G為頂點的三角形相似,求t的值;
(3)是否存在實數t,使得點B’與點O重合?若存在,求出t的值;若不存在,請說明理由.
【答案】(1)t=1.25;(2)當t=1.4s或t=(﹣7+![]() )s時,以點E、B、F為頂點的三角形與以點F,C,G為頂點的三角形相似;(3)不存在實數t,使得點B′與點O重合.理由見解析.
)s時,以點E、B、F為頂點的三角形與以點F,C,G為頂點的三角形相似;(3)不存在實數t,使得點B′與點O重合.理由見解析.
【解析】
(1)利用正方形的性質,得到BE=BF,列一元一次方程求解即可;
(2)△EBF與△FCG相似,分兩種情況,需要分類討論,逐一分析計算;
(3)本問為存在型問題.假設存在,則可以分別求出在不同條件下的t值,它們互相矛盾,所以不存在
(1)若四邊形EBFB′為正方形,則BE=BF,BE=5﹣t,BF=3t,
即:5﹣t=3t,
解得t=1.25;
故答案為:1.25;
(2)分兩種情況,討論如下:
①若△EBF∽△FCG,
則有![]() ,即
,即![]() ,
,
解得:t=1.4;
②若△EBF∽△GCF,
則有![]() ,即
,即![]() ,
,
解得:t=﹣7﹣![]() (不合題意,舍去)或t=﹣7+
(不合題意,舍去)或t=﹣7+![]() .
.
∴當t=1.4s或t=(﹣7+![]() )s時,以點E、B、F為頂點的三角形與以點F,C,G為頂點的三角形相似.
)s時,以點E、B、F為頂點的三角形與以點F,C,G為頂點的三角形相似.
(3)假設存在實數t,使得點B′與點O重合.
如圖,過點O作OM⊥BC于點M,則在Rt△OFM中,OF=BF=3t,FM=![]() BC﹣BF=3﹣3t,OM=2.5,
BC﹣BF=3﹣3t,OM=2.5,
由勾股定理得:OM2+FM2=OF2,
即:2.52+(3﹣3t)2=(3t)2
解得:t=![]() ;
;
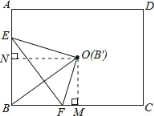
過點O作ON⊥AB于點N,則在Rt△OEN中,OE=BE=5﹣t,EN=BE﹣BN=5﹣t﹣2.5=2.5﹣t,ON=3,
由勾股定理得:ON2+EN2=OE2,
即:32+(2.5﹣t)2=(5﹣t)2
解得:t=![]() .
.
∵![]() ≠
≠![]() ,
,
∴不存在實數t,使得點B′與點O重合.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】某校興趣小組就“最想去的金華最美村落”隨機調查了本校部分學生,要求每位同學選擇且只能選擇一個最想去的最美鄉村![]() 下面是根據調查結果繪制出的不完整的統計圖
下面是根據調查結果繪制出的不完整的統計圖
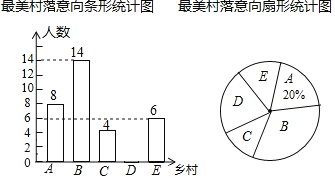
請根據圖中提供的信息,解答下列問題:
![]() 被調查的學生總人數為______人;
被調查的學生總人數為______人;
![]() 扇形統計圖中“最想去鄉村D”的扇形圓心角的度數為______;
扇形統計圖中“最想去鄉村D”的扇形圓心角的度數為______;
![]() 若該校共有800名學生,請估計“最想去鄉村B”的學生人數.
若該校共有800名學生,請估計“最想去鄉村B”的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:求1+2+22+23+24+…+22017
首先設S=1+2+22+23+24+…+22017 ① 則2S=2+22+23+24+25+…+22018 ②
②﹣①得S=22018﹣1 即1+2+22+23+24+…+22017=22018﹣1
以上解法,在數列求和中,我們稱之為:“錯位相減法”
請你根據上面的材料,解決下列問題
(1)求1+3+32+33+34+…+32019的值
(2)若a為正整數且![]() ,求
,求![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年的6月5日為世界環保日,為了提倡低碳環保,某公司決定購買10臺節省能源的新設備,現有甲、乙兩種型號的設備可供選購. 經調查:購買3臺甲型設備比購買2臺乙型設備多花16萬元,購買2臺甲型設備比購買3臺乙型設備少花6萬元.
(1)求甲、乙兩種型號設備的價格;
(2)該公司經預算決定購買節省能源的新設備的資金不超過110萬元,你認為該公司有哪幾種購買方案;
(3)在(2)的條件下,已知甲型設備的產量為240噸/月,乙型設備的產量為180噸/月.若每月要求總產量不低于2040噸,為了節約資金,請你為該公司設計一種最省錢的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D,E在線段BC上,△ADE是等邊三角形,且∠BAC=120°
(1)求證:△ABD∽△CAE;
(2)若BD=2,CE=8,求BC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
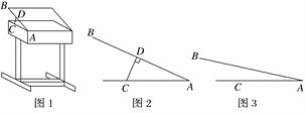
【題目】某課桌生產廠家研究發現,傾斜12°~24°的桌面有利于學生保持軀體自然姿勢.根據這一研究,廠家決定將水平桌面做成可調節角度的桌面.新桌面的設計圖如圖1,AB可繞點A旋轉,在點C處安裝一根可旋轉的支撐臂CD,AC=30 cm.
(1)如圖2,當∠BAC=24°時,CD⊥AB,求支撐臂CD的長;
(2)如圖3,當∠BAC=12°時,求AD的長.(結果保留根號)
(參考數據:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
科目:初中數學 來源: 題型:
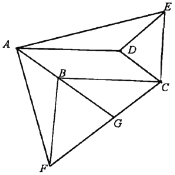
【題目】如圖,在口ABCD中,分別以邊BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,連接AF,AE.
(1)求證:△ABF≌△EDA;
(2)延長AB與CF相交于G,若AF⊥AE,求證BF⊥BC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com