
【題目】已知數軸上兩點A、B所表示的數分別為a和b,且滿足|a+3|+(b-9)2018=0,O為原點
(1) 試求a和b的值
(2) 點C從O點出發向右運動,經過3秒后點C到A點的距離是點C到B點距離的3倍,求點C的運動速度?
(3) 點D以1個單位每秒的速度從點O向右運動,同時點P從點A出發以5個單位每秒的速度向左運動,點Q從點B出發,以20個單位每秒的速度向右運動.在運動過程中,M、N分別為PD、OQ的中點,問![]() 的值是否發生變化,請說明理由.
的值是否發生變化,請說明理由.
【答案】(1) a=-3,b=9;(2)每秒5個單位或每秒2個單位;(3) ![]() 為定值,理由見解析
為定值,理由見解析
【解析】
(1) 根據非負數的和等于零,可得每個非負數同時為零,從而a=-3,b=9;
(2)設C點對應的數為x,CA=x-(-3)=x+3,由于點C存在在B點左側和右側兩種情況,故CB的長為|x-9|,根據CA=3CB列式即可求出x,從而求得運動速度;
(3設運動時間為t秒,用含t的代數式分別表示PQ、OD、MN,然后代入![]() 求值即可判斷.
求值即可判斷.
(1) a=-3,b=9
(2) 設3秒后,點C對應的數為x
則CA=|x+3|,CB=|x-9|
∵CA=3CB
∴|x+3|=3|x-9|=|3x-27|
當x+3=3x-27,解得x=15,此時點C的速度為![]()
當x+3+3x-27=0,解得x=6,此時點C的速度為![]()
(3) 設運動的時間為t
點D對應的數為:t
點P對應的數為:-3-5t
點Q對應的數為:9+20t
點M對應的數為:-1.5-2t
點N對應的數為:4.5+10t
則PQ=25t+12,OD=t,MN=12t+6
∴![]() 為定值.
為定值.
故答案為:(1) a=-3,b=9;(2)每秒5個單位或每秒2個單位;(3) ![]() 為定值.
為定值.


科目:初中數學 來源: 題型:
【題目】已知:直線y=﹣x﹣4分別交x、y軸于A、C兩點,拋物線y=ax2+bx(a>0)經過A、O兩點,且頂點B的縱坐標為﹣2 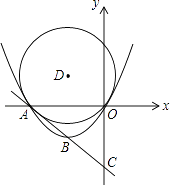
(1)判斷點B是否在直線AC上,并求該拋物線的函數關系式;
(2)以點B關于x軸的對稱點D為圓心,以OD為半徑作⊙D,試判斷直線AC與⊙D的位置關系,并說明理由;
(3)若E為⊙D的優弧AO上一動點(不與A、O重合),連結AE、OE,問在拋物線上是否存在點P,使∠POA:∠AEO=2:3?若存在,請求出所有滿足條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某玩具廠熟練工人工資為:每月底薪700元,加獎勵工資按件計算,一個月工作日為25天,每天工作8小時,加工1件A種玩具計酬10元,加工1件B種玩具計酬8元.在工作中發現一名熟練工人加工1件A種玩具和2件B種玩具需4小時,加工3件A種玩具和1件B種玩具需7小時.(工人月工資=底薪+計件工資)
(1)求熟練工人每加工一件A種玩具和一件B種玩具,分別需要多少時間?
(2)深圳市規定最低工資標準為每月2030元,但玩具廠規定:“每名工人每月必須加工A、B兩種工具,且加工A種玩具數量不少于B種玩具的一半”.若設一名熟練工人每月加工A種玩具a件,工資總額為w元,請你運用所學知識判斷該公司在執行規定后是否違背了深圳市最低工資標準?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,下列說法錯誤的是( ) 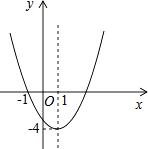
A.圖象關于直線x=1對稱
B.函數y=ax2+bx+c(a≠0)的最小值是﹣4
C.﹣1和3是方程ax2+bx+c=0(a≠0)的兩個根
D.當x<1時,y隨x的增大而增大
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某愛心企業在政府的支持下投入資金,準備修建一批室外簡易的足球場和籃球場,供市民免費使用,修建1個足球場和1個籃球場共需8.5萬元,修建2個足球場和4個籃球場共需27萬元.
(1)求修建一個足球場和一個籃球場各需多少萬元?
(2)該企業預計修建這樣的足球場和籃球場共20個,投入資金不超過90萬元,求至少可以修建多少個足球場?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們定義三個有理數之間的新運算法則“⊕”:a⊕b⊕c=![]() (|a﹣b﹣c|+a+b+c),如:1⊕(﹣2)⊕3=
(|a﹣b﹣c|+a+b+c),如:1⊕(﹣2)⊕3=![]() [|1﹣(﹣2)﹣3|+1+(﹣2)+3]=l,在﹣2,﹣4,﹣5,0,2,5,6這7個數中,任意取三個數作為a,b,c的值,進行“a⊕b⊕c“運算,求在所有計算的結果中的最大值是_____.
[|1﹣(﹣2)﹣3|+1+(﹣2)+3]=l,在﹣2,﹣4,﹣5,0,2,5,6這7個數中,任意取三個數作為a,b,c的值,進行“a⊕b⊕c“運算,求在所有計算的結果中的最大值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某游泳池有水4000m3 , 先放水清洗池子.同時,工作人員記錄放水的時間x(單位:分鐘)與池內水量y(單位:m3) 的對應變化的情況,如下表:
時間x(分鐘) | … | 10 | 20 | 30 | 40 | … |
水量y(m3) | … | 3750 | 3500 | 3250 | 3000 | … |
(1)根據上表提供的信息,當放水到第80分鐘時,池內有水多少m3?
(2)請你用函數解析式表示y與x的關系,并寫出自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線a∥b,直線c與a、b都相交,從所標識的∠1、∠2、∠3、∠4、∠5這五個角中任意選取兩個角,則所選取的兩個角互為補角的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com