若AD是等腰△ABC一腰上的高，且∠DAB=60°，則△ABC的三個角的度數分別是________．
∠BAC=15°，∠B=150°，∠C=15°或∠BAC=75°，∠B=30°，∠C=75°或∠BAC=30°，∠B=30°，∠C=120°
分析：題中沒有指明哪個是底哪個是腰，也沒有指明這個三角形是什么形狀，故應該分情況進行分析．
解答：
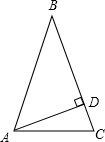
解：①如圖，∵∠DAB=60°，∠ADB=90°，
∴∠B=30°，
∵AB=BC，
∴∠BAC=∠C=75°．
②如圖，∵∠DAB=60°，∠ADB=90°，
∴∠DBA=30°，
∵AB=BC，
∴∠BAC=∠C=15°，∠B=150°．
③如圖，∵∠DAB=60°，∠ADB=90°，
∴∠B=30°，
∵AC=BC，
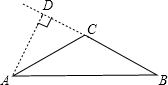
∴∠BAC=∠B=30°，∠C=120°．
故答案為：∠BAC=15°，∠B=150°，∠C=15°或∠BAC=75°，∠B=30°，∠C=75°或∠BAC=30°，∠B=30°，∠C=120°．
點評：此題主要考查等腰三角形的性質，三角形內角和定理及三角形外角性質的綜合運用，注意分類討論思想的運用．
