
在一條直線上依次有A、B、C三個港口,甲、乙兩船同時分別從A、B港口出發,沿直線勻速駛向C港.最終到達C港.設甲、乙兩船行駛x(h)后,與B港的距離分別為y1、y2(km),y1、y2與x的函數關系如圖.
(1)填空:A、C兩港口間的距離為 km,a= ;
(2)請分別求出y1、y2與x的函數關系式,并求出交點P的坐標;
(3)若兩船的距離不超過10km時能夠相互望見,求甲、乙兩船經過多長時間正好相距10千米?
(1)120,4;(2)y1= ,y2=15x(0≤x≤6),點P的坐標為(2,30);(3)甲、乙兩船經過
,y2=15x(0≤x≤6),點P的坐標為(2,30);(3)甲、乙兩船經過 小時或
小時或 小時或
小時或 小時,正好相距10千米.
小時,正好相距10千米.
解析試題分析:(1)從圖中可以看出A、B兩港是30km,B、C兩港是90km,A、C兩港口間的距離為30+90=120km,根據路程÷時間求出甲的速度:30÷1=30(km/h),進而求出a的值:a=120÷30=4.
(2)利用待定系數法求出y1,y2,聯立解方程組,即可求出點P的坐標.
(3)先根據一次函數的圖象求出乙的速度,再根據甲在乙船前和乙船后,及甲船已經到了而乙船正在行駛,三種情況進行解答即可.
試題解析:(1)120,4.
(2)當0≤x≤1時,由點(0,30),(1,0)求得y1=﹣30x+30;
當1<x≤4時,由點(1,0),(4,90)求得y1=30x﹣30;
即y1與x的函數關系式為y1= .
.
由點(6,90)求得,y2=15x(0≤x≤6),
即y2與x的函數關系式為y2=15x(0≤x≤6);
由圖象可知,交點P的橫坐標x>1,此時y1=y2,
解方程組 ,得
,得 .
.
所以點P的坐標為(2,30);
(3)由函數圖象可知,乙船的速度為:90÷6=15(km/m).
①甲在乙后10km,設行駛時間為xh,則x<2.
如果0≤x≤1,那么(﹣30x+30)+15x=10,解得x= ,不合題意舍去;
,不合題意舍去;
如果1≤x<2,那么15x﹣(30x﹣30)=10,解得x= ,符合題意;
,符合題意;
②甲超過乙后,甲在乙前10km,設行駛時間為xh,則x>2.
由題意,得30x﹣30﹣15x=10,解得x= ,符合題意;
,符合題意;
③甲船已經到了而乙船正在行駛,則4≤x<6.
由題意,得90﹣15x=10,解得x= ,符合題意;
,符合題意;
即甲、乙兩船經過 小時或
小時或 小時或
小時或 小時,正好相距10千米.
小時,正好相距10千米.
考點:1.一次函數的應用;2.直線上點的坐標與方程的關系;3.待定系數法的應用;4.分類思想的應用..


科目:初中數學 來源: 題型:解答題
某市為了鼓勵居民節約用水,采用分段計費的方法按月計算每戶家庭的水費,月用水量不超過20m3時,按2元/m3計算;月用水量超過20m3時,超過部分按2.6元/m3計費。設每戶家庭用水量為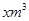 時,應交水費y元。
時,應交水費y元。
(1)分別求出 和
和 時y與x的關系式;
時y與x的關系式;
(2)小明家第二季度交納水費的情況如下:
| 月份 | 四月份 | 五月份 | 六月份 |
| 交費金額 | 30元 | 34元 | 42.6元 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,一次函數y=﹣x+2的圖象與反比例函數y=﹣ 的圖象交于A、B兩點,與x軸交于D點,且C、D兩點關于y軸對稱.
的圖象交于A、B兩點,與x軸交于D點,且C、D兩點關于y軸對稱.
(1)求A、B兩點的坐標;
(2)求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知一次函數y=kx+b,當x=2時,y=﹣3,當x=1時,y=﹣1.
(1)求一次函數的解析式;
(2)若該一次函數的圖形交x軸y軸分別于A、B兩點,求△ABO的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,正方形的邊長為4,P為正方形邊上一動點,運動路線是A→D→C→B→A,設P點經過的路程為x,以點A、P、D為頂點的三角形的面積是y.則下列圖象能大致反映y與x的函數關系的是( )
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在平面直角坐標系xOy中,一次函數y=ax+b的圖象與x軸相交于點A(-2,0),與y軸交于點C,與反比例函數 在第一象限內的圖象交于點B(m,n),連結OB.若S△AOB=6,S△BOC=2.
在第一象限內的圖象交于點B(m,n),連結OB.若S△AOB=6,S△BOC=2.
(1)求一次函數的表達式;
(2)求反比例函數的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
下表中,y是x的一次函數.
| x |  2 2 | 1 | 2 | | 5 |
| y | 6 |  3 3 | |  12 12 |  15 15 |
 圖象上,求這兩個函數圖象的另一交點N的坐標.
圖象上,求這兩個函數圖象的另一交點N的坐標.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
無論k取任何實數,對于直線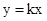 都會經過一個固定的點
都會經過一個固定的點 ,我們就稱直線
,我們就稱直線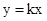 恒過定點
恒過定點 .
.
(1)無論 取任何實數,拋物線
取任何實數,拋物線 恒過定點
恒過定點 ,直接寫出定點A的坐標;
,直接寫出定點A的坐標;
(2)已知△ABC的一個頂點是(1)中的定點 ,且∠B,∠C的角平分線分別是y軸和直線
,且∠B,∠C的角平分線分別是y軸和直線 ,求邊BC所在直線的表達式;
,求邊BC所在直線的表達式;
(3)求△ABC內切圓的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
甲、乙兩人騎車前往A地,他們距A地的路程S(km)與行駛時間t(h)之間的關系如圖所示,請根據圖象所提供的信息解答下列問題:
(1)、甲、乙兩人的速度各是多少?
(2)、求甲距A地的路程S與行駛時間t的函數關系式。
(3)、直接寫出在什么時間段內乙比甲距離A 地更近?(用不等式表示)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com