已知△ABC是非等腰直角三角形,∠BAC=90°,在BC所在直線上取兩點D、E,使BD=BC=CE,連接AD、AE;已知∠BAD=45°,那么tan∠CAE=________.

分析:過B、C兩點作BM∥AC,CN∥AB,由中位線可得AC=2BM,AB=2CN,則tan∠BAD•tan∠CAE=

,又45°角所對的正切值為1,進而即可求出結論.
解答:如圖,過B、C兩點作BM∥AC,CN∥AB分別交AD、AE于M、N,
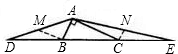
∵BD=BC,即點B為CD的中點,
∴AC=2BM,
同理AB=2CN,又tan∠BAD=
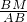
,tan∠CAE=
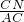
,從而
tan∠BAD•tan∠CAE=

,
∵tan∠BAD=1,
∴tan∠CAE=

.
故答案為

.
點評:本題主要考查了平行線分線段成比例的性質問題以及三角函數的一些基礎知識,能夠掌握并熟練運用.
