Question

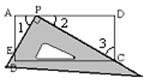
如圖，在矩形ABCD中，AB＝4，AD＝10．一把三角尺的直角頂點P在AD上滑動時（點P與A、D不重合），一直角邊始終經過點C，另一直角邊與AB交于點E．

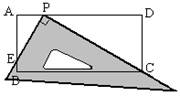
（1）證明△DPC∽△AEP；

（2）當∠CPD＝30°時，求AE的長；

（3）是否存在這樣的點P，使△DPC的周長等于△AEP周長的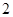倍？若存在，求出DP的長；若不存在，請說明理由．

 

Answer 1

【答案】

(1)詳見解析；（2）AE=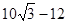；(3)DP=8.

【解析】

試題分析：(1)兩個三角形都是直角三角形，所以有一角相等，再根據圖中的條件，再求出一對對應角相等，就可以得到△DPC∽△AEP；（2）在△CDP中，根據直角三角形中，30°的角所對的直角邊等于斜邊的一半，可知PC=8,再根據勾股定理得PD=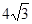,然后利用相似三角形的對應邊的比相等，即可求出AE的值；（3）因為相似三角形的周長比等于相似比，所以只要△DPC的邊CD等于△PAE的邊AP的2倍，那么△DPC的周長等于△AEP周長的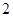倍.

試題解析：（1）在△DPC、△AEP中，∠1與∠2互余，∠2與∠3互余，∴∠1＝∠3 

又∠A＝∠D＝90°，∴△DPC∽△AEP

（2）∵∠2＝30°，CD＝4，∴PC＝8，PD＝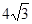

由(1)得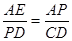：,所以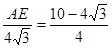,所以AE=.

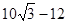（3）存在這樣的點P，使△DPC的周長等于△AEP周長的2倍，

∵相似三角形周長的比等于相似比，設，解得DP＝8

考點：1、相似三角形的判定；2、相似三角形的性質.