
如下圖,⊙O1與⊙O2相交于A、B兩點,過點A作直線CD∥O1O2,交⊙O1于點C,交⊙O2于點D.
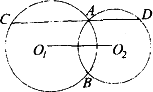
求證:CD=2O1O2.
|
證明:連結AB、BC、BD. ∵AB是⊙O1與⊙O1的公共弦, ∴AB⊥O1O2, ∵CD∥O1O2, ∴AB⊥CD于A,∴∠CAB=90°. ∴BC是⊙O1的直徑. ∴O1是BC的中點. 同理可證O2是BD的中點. ∴CD=2O1O2. 思路點撥:要證明CD=2O1O2,由已知條件CD∥O1O2,若能以CD為邊造出一個三角形,使得O1O2成為這個三角形的中位線,那么本題便可獲得證明.考慮到點O1和點O2分別是兩圓圓心,連結BC、BD,如果能證得BC、BD分別是兩圓的直徑,即可說明點O1和點O2分別是BC、BD的中點,這樣解決問題的關鍵也就是要證明BC、BD分別是⊙O1與⊙O2的直徑,要證明圓的一條弦是圓的直徑,常用的方法是證明此弦所對的圓周角是直角,由此可聯想到“相交兩圓的連心線垂直平分公共弦”這一性質,這樣就不難得出BC、BD是兩圓⊙O1與⊙O2的直徑這一結論.
評注:在兩圓相交時,一方面公共弦是常作的輔助線,因為通過公共弦可以把兩圓聯系起來,是溝通兩圓的一座橋梁,另一方面而且由于連心線垂直平分公共弦,又能構造直角三角形,既能證明弦是直徑,又可解決有關計算問題. |


科目:初中數學 來源:宿遷市修遠中學2007-2008學年度初三年級第一學期期中考試數學試卷(含答案) 題型:013
如下圖,⊙O1與⊙O2內切,半徑分別為3和1,作⊙O2的切線,切點為A,則O1A的長為

A.2
B.4
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源:初中數學解題思路與方法 題型:044
已知如下圖,⊙O1與⊙O2相交于A、B兩點,⊙O1經過點O2,E是⊙O1優弧![]() 上的一點,O2E交⊙O2于C,交AB于D,又知CD=1,CE=2,求O2E∶O2D.
上的一點,O2E交⊙O2于C,交AB于D,又知CD=1,CE=2,求O2E∶O2D.
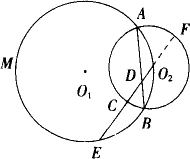
查看答案和解析>>
科目:初中數學 來源:初中數學解題思路與方法 題型:044
已知如下圖,⊙O1與⊙O2外切于點P,A為⊙O1上一點,直線AC切⊙O2于點C,交⊙O1于點B,AP的延長線交⊙O2于點D.若⊙O1半徑是⊙O2半徑的2倍,PD=10,AB=7![]() ,求PC的長.
,求PC的長.
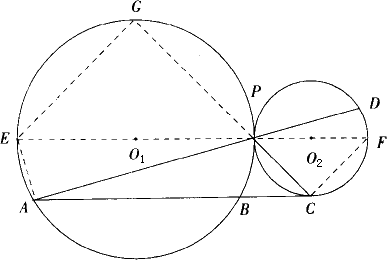
查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(湖北黃石卷)數學(解析版) 題型:填空題
如下圖,在邊長為3的正方形ABCD中,圓O1與圓O2外切,且圓O1分別與DA、DC邊相切,圓O2分別與BA、BC邊相切,則圓心距O1O2為 .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com