
【題目】如圖,點A(﹣2,0)、B(4,0)、C(3,3)在拋物線y=ax2+bx+c上,點D在y軸上,且DC⊥BC,∠BCD繞點C順時針旋轉后兩邊與x軸、y軸分別相交于點E、F.
(1)求拋物線的解析式;
(2)CF能否經過拋物線的頂點?若能,求出此時點E的坐標;若不能,說明理由;
(3)若△FDC是等腰三角形,求點F的坐標.
【答案】
(1)
解:由拋物線與X軸的兩個交點A、B的坐標,
可以由兩根式設拋物線解析式為:y=a(x+2)(x﹣4),
然后將C點坐標代入得:a(3+2)(3﹣4)=3,
解得:a=﹣ ![]() ,
,
故拋物線解析式是:y=﹣ ![]() (x+2)(x﹣4)
(x+2)(x﹣4)

(2)
解:由C、B兩點坐標利用待定系數法可以求得CB直線方程為:y=﹣3x+12,
∵CD⊥CB,
∴CD直線方程可以設為:
y= ![]() x+m,
x+m,
將C點坐標代入得:m=2,
∴CD直線方程為:y= ![]() x+2,
x+2,
∴D點坐標為:D(0,2),
由拋物線解析式可以頂點公式或對稱軸x=1解得頂點M坐標為M(1, ![]() ),
),
∴由C、M兩點坐標可以求得CM即CF直線方程為:y=﹣ ![]() x+
x+ ![]() ,
,
∴F點坐標為:F(0, ![]() ),
),
∴CE直線方程可以設為:y= ![]() x+n,
x+n,
將C點坐標代入得:n= ![]() ,
,
∴CE直線方程為:y= ![]() x+
x+ ![]() ,
,
令y=0,解得:x=﹣ ![]() ,
,
∴E點坐標為E(﹣ ![]() ,0),
,0),
∴能;
(3)
解:由C、D兩點坐標可以求得CD= ![]() ,
,
則△FDC是等腰△可以有三種情形:
① FD=CD= ![]() ,
,
則F點坐標為F(0,2+ ![]() ),
),
②FC=CD= ![]() ,過C點作y軸垂線,垂足為H點,
,過C點作y軸垂線,垂足為H點,
則DH=1,
則FH=1,
則F點坐標為F(0,4),
③FD=FC,作DC的中垂線FG,交y軸于F點,交DC于G點,
由中點公式得G點坐標為G( ![]() ,
, ![]() ),
),
由DC兩點可以求得DC直線方程為:y= ![]() x+2,
x+2,
則FG直線方程可以設為:y=﹣3x+p,
將G點坐標代入解得:p=7,
故F點坐標為(0,7).
【解析】(1)由拋物線與X軸的兩個交點A、B的坐標,可以由兩根式設拋物線解析式為:y=a(x+2)(x﹣4),求出a的值即可;(2)由C、B兩點坐標利用待定系數法可以求得CB直線方程為:y=﹣3x+12,設CD直線方程可以設為:y= ![]() x+m,求出m的值,進而求出D點的值,由拋物線解析式可以頂點公式或對稱軸x=1解得頂點M坐標,由C、M兩點坐標可以求得CM即CF直線方程,CE直線方程可以設為:y=
x+m,求出m的值,進而求出D點的值,由拋物線解析式可以頂點公式或對稱軸x=1解得頂點M坐標,由C、M兩點坐標可以求得CM即CF直線方程,CE直線方程可以設為:y= ![]() x+n,求出n的值,進而求出E點的坐標;(3)由C、D兩點坐標可以求得CD=
x+n,求出n的值,進而求出E點的坐標;(3)由C、D兩點坐標可以求得CD= ![]() ,△FDC是等腰△可以有三種情形:①當FD=CD;②FC=CD;③FD=FC,分別求出F點的坐標即可;
,△FDC是等腰△可以有三種情形:①當FD=CD;②FC=CD;③FD=FC,分別求出F點的坐標即可;


科目:初中數學 來源: 題型:
【題目】某中學積極開展“陽光體育”活動,共開設了跳繩、乒乓球、籃球、跑步四種運動項目.為了解學生最喜愛哪一種項目,隨機抽取了部分學生進行調查,并繪制了如下的條形統計圖和扇形統計圖(部分信息未給出)
(1)求本次被調查的學生人數;
(2)補全條形統計圖;
(3)根據統計的數據估計該中學3200名學生中最喜愛籃球的人數約有_____人.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,補充條件后仍不一定能保證△ABC≌△A′B′C′,則補充的這個條件是( )

A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】星期天,李玉剛同學隨爸爸媽媽會老家探望爺爺奶奶,爸爸8:30騎自行車先走,平均每小時騎行20km;李玉剛同學和媽媽9:30乘公交車后行,公交車平均速度是40km/h.爸爸的騎行路線與李玉剛同學和媽媽的乘車路線相同,路程均為40km/h.設爸爸騎行時間為x(h).
(1)請分別寫出爸爸的騎行路程y1(km)、李玉剛同學和媽媽的乘車路程y2(km)與x(h)之間的函數解析式,并注明自變量的取值范圍;
(2)請在同一個平面直角坐標系中畫出(1)中兩個函數的圖象;
(3)請回答誰先到達老家.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店購進甲、乙兩種商品,購進 4 件甲種商品比購進 5 件乙種商品少用 10 元,購 進 20 件甲種商品和 10 件乙種商品共用去 160 元.
(1)求甲、乙兩種商品每件進價分別是多少元?
(2)若該商店購進甲、乙兩種商品共 140 件,都標價 10 元出售,售出一部分降價促銷, 以標價的八折售完所有剩余商品,以 10 元售出的商品件數比購進甲種商品件數少 20 件,該商店此次購進甲、乙兩種商品降價前后共獲利不少于 420 元,求至少購進甲種商品多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】勾股定理是一條古老的數學定理,它有很多種證明方法,我國漢代數學家趙爽根據弦圖,利用面積法進行證明,著名數學家華羅庚曾提出把“數形關系”(勾股定理)帶到其他星球,作為地球人與其他星球“人”進行第一次“談話”的語言.
[定理表述]
請你寫出勾股定理內容(用文字語言表述):
[嘗試證明]
以圖1中的直角三角形為基礎,可以構造出以a、b為底,以(a+b)為高的直角梯形(如圖2),請你利用圖2,證明勾股定理.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD是△ABC的角平分線,DE,DF分別是△ABD和△ACD的高,得到下面四個結論:①OA=OD;②AD⊥EF;③當∠BAC=90°時,四邊形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正確的是_________.(填序號)
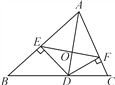
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC中,∠BCA=90°,BC=AC,D是BA邊上一點(點D不與A,B重合),M是CA中點,當以CD為直徑的⊙O與BA邊交于點N,⊙O與射線NM交于點E,連接CE,DE. 
(1)求證:BN=AN;
(2)猜想線段CD與DE的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2016山西省)我省某蘋果基地銷售優質蘋果,該基地對需要送貨且購買量在2000kg﹣5000kg(含2000kg和5000kg)的客戶有兩種銷售方案(客戶只能選擇其中一種方案):
方案A:每千克5.8元,由基地免費送貨.
方案B:每千克5元,客戶需支付運費2000元.
(1)請分別寫出按方案A,方案B購買這種蘋果的應付款y(元)與購買量x(kg)之間的函數表達式;
(2)求購買量x在什么范圍時,選用方案A比方案B付款少;
(3)某水果批發商計劃用20000元,選用這兩種方案中的一種,購買盡可能多的這種蘋果,請直接寫出他應選擇哪種方案.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com