【題目】在平面直角坐標系中，拋物線
的圖像與x軸交于B,C兩點（B在C的左側），與y軸交于點A。
（1）求出點A,B,C的坐標。
（2）向右平移拋物線，使平移后的拋物線恰好經過△ABC的外心，求出平移后的拋物線的解析式.
【答案】（1）A(0,4), B(-2,0), C(8,0) ；(2) 
【解析】
（1）根據二次函數與一元二次方程的關系,令y=0,可得:,
,解得:
,繼而求出B(-2,0), C(8,0), 令x=0,則y=4,繼而求出A(0,4),
(2) 根據
,因此可得:
,根據勾股定理逆定理可得:△ABC是直角三角形,根據直角三角形性質可得:△ABC的外心為（3,0）,
再根據二次函數圖象平移可得:拋物線向右平移5個單位,平移后的拋物線為:
.
（1）A(0,4), B(-2,0), C(8,0),
(2) ∵ ,
∴,
∴△ABC是直角三角形,
∴△ABC的外心為（3,0）,
∴拋物線向右平移5個單位,
平移后的拋物線為:.
新思維寒假作業系列答案科目：初中數學 來源： 題型：
【題目】已知，拋物線y＝﹣x2+bx+c經過點A（﹣1，0）和C（0，3）．（1）求拋物線的解析式；（2）在拋物線的對稱軸上，是否存在點P，使PA+PC的值最小？如果存在，請求出點P的坐標，如果不存在，請說明理由；（3）設點M在拋物線的對稱軸上，當△MAC是直角三角形時，求點M的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知某項工程由甲乙兩隊合作12天可以完成,供需工程費用13800元,乙隊單獨完成這項工程所需時間是甲隊單獨完成這項工程所需時間的1.5倍,且甲隊每天的工程費用比乙隊多150元。
（1）甲乙兩隊單獨完成這項工程分別需要多少天?
（2）若工程管理部門決定從這兩個隊中選一個隊單獨完成這項工程,從節約資金的角度考慮,應該選擇哪個工程隊?請說明理由。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一客車一出租車分別從甲乙兩地相向而行同時出發，設客車離甲地距離為y1千米，出租車離甲地距離為y2千米，兩車行駛的時間為x小時，y1、y2關于的函數圖象如圖所示：
（1）根據圖象，直接寫出y1、y2關于x的關系式；
（2）求經過多少小時，兩車之間的距離為120千米？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,在平面直角坐標系中,邊長為1的正方形OA1B1C1的兩邊在坐標軸上,以它的對角線OB1為邊作正方形OB1B2C2再以正方形OB1B2C2的對角線OB2為邊作正方形OB2B3C3,以此類推、則正方形OB2018B2019C2019的頂點B2019的坐標是______________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某中學舉辦了綠色閱讀節活動，為了表彰優秀，陳老師負責購買獎品，在購買時他發現身上所帶的錢：若以2支鋼筆和3個筆記本為一份獎品，則可買50份獎品；若以2支鋼筆和6本筆記本為一份獎品，則可以買40份獎品，設鋼筆單價為
元/支，筆記本單價為
元/支．
（1）請用含的代數式表示；
（2）若用這筆錢全部購買筆記本，總共可以買幾本？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，△ABC中，CD⊥AB于D，且BD : AD : CD＝2 : 3 : 4，
（1）試說明△ABC是等腰三角形；
（2）已知S△ABC＝40cm2，如圖2，動點M從點B出發以每秒2cm的速度沿線段BA向點A 運動，同時動點N從點A出發以每秒1cm速度沿線段AC向點C運動，當其中一點到達終點時整個運動都停止. 設點M運動的時間為t（秒），
①若△DMN的邊與BC平行，求t的值；
②若點E是邊AC的中點，問在點M運動的過程中，△MDE能否成為等腰三角形？若能，求出t的值；若不能，請說明理由．
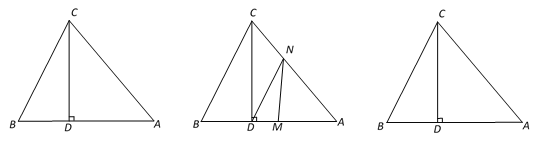
圖1 圖2 備用圖
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平面直角坐標系
中
，
，
．
（1）作出
關于直線
對稱的圖形△
并寫出△各頂點的坐標；
（2）將△向左平移2個單位，作出平移后的△
，并寫出△各頂點的坐標；
（3）觀察和△，它們是否關于某直線對稱？若是，請指出對稱軸，并求的面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
