
【題目】有這樣一個問題:探究函數![]() 的圖象與性質.小華根據學習函數的經驗,對函數
的圖象與性質.小華根據學習函數的經驗,對函數![]() 的圖象與性質進行了探究.下面是小華的探究過程,請補充完整:
的圖象與性質進行了探究.下面是小華的探究過程,請補充完整:
(1)函數![]() 的自變量x的取值范圍是___________;
的自變量x的取值范圍是___________;
(2)下表是y與x的幾組對應值.m的值為_______;
x | -2 |
| -1 |
|
|
| 1 | 2 | 3 | 4 | … |
y | 0 |
| m |
|
|
|
| 1 |
|
| … |
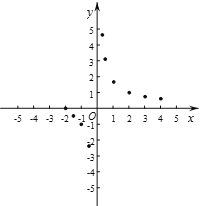
(3)如圖,在平面直角坐標系xOy中,描出了以上表中各對對應值為坐標的點.根據描出的點,畫出該函數的圖象;
(4)結合函數的圖象,寫出該函數的一條性質:____________.
(5)結合函數圖象估計![]() 的解的個數為_______個.
的解的個數為_______個.
【答案】(1)x≥-2且x≠0;(2)-1;(3)見詳解;(4)當2≤x<0或x>0時,y隨x增大而減小,答案不唯一;(5)1
【解析】
(1)根據分式有意義分母不為0和二次根式有意義的條件被開方數非負,即可得出關于x的一元一次不等式組,解之即求出自變量x的取值范圍;
(2)將x=-1代入解析式求m的值即可;
(3)根據圖中描出各點,連點成線畫出圖象即可;
(4)觀察函數圖象,根據函數圖象可尋找到函數具有性質;
(5)在第(3)基礎上做出函數y=x+4的圖象,數出它們的交點個數,
解:(1)根據題意得,x+2≥0且x≠0
解得:x≥-2且x≠0
∴函數![]() 的自變量x的取值范圍是:x≥-2且x≠0
的自變量x的取值范圍是:x≥-2且x≠0
(2)當x=-1時,m=![]() ,
,
∴m=-1
(3)圖象如圖所示:
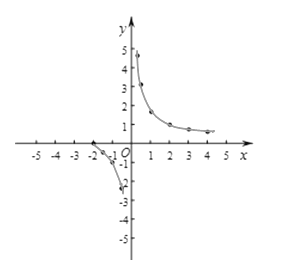
(4)在-2≤x<0時,函數隨著x的增大而減小,在x>0時,y隨著x的增大而減小;
故答案為:當2≤x<0或x>0時,y隨x增大而減小.
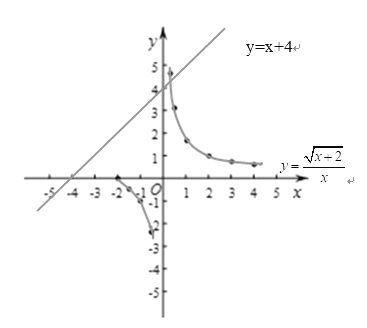
(5)∵方程組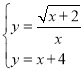 的解為兩個函數圖象的交點,兩函數圖象如下圖,
的解為兩個函數圖象的交點,兩函數圖象如下圖,
也就是圖象中的交點個數只有一個
∴方程![]() 的解的個數也是1個
的解的個數也是1個


科目:初中數學 來源: 題型:
【題目】下列條件能判定△ABC≌△DEF的是( )
A. AB=DE AC=DF ∠B=∠EB. AB=DE AC=DF ∠C=∠F
C. AB=DE AC=DF ∠A=∠DD. AB=DE AC=DF ∠B=∠F
查看答案和解析>>
科目:初中數學 來源: 題型:
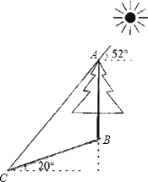
【題目】如圖,在一個坡角為20°的斜坡上有一棵樹,高為AB,當太陽光線與水平線成52°角時,測得該樹斜坡上的樹影BC的長為10m,求樹高AB(精確到0.1m) (已知:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364,sin52°≈0.788,cos52°≈0.616,tan52°≈1.280.供選用)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程mx2-(m+2)x+2=0(m≠0)
(1)求證:方程一定有兩個實數根;
(2)若此方程的兩根為不相等的整數,求整數m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果關于![]() 的一元二次方程
的一元二次方程![]() 有兩個實數根,且其中一個根為另一個根的2倍,則稱這樣的方程為“倍根方程”,研究發現了此類方程的一般性結論:設其中一根為
有兩個實數根,且其中一個根為另一個根的2倍,則稱這樣的方程為“倍根方程”,研究發現了此類方程的一般性結論:設其中一根為![]() ,則另一個根為
,則另一個根為![]() ,因此
,因此![]() ,所以有
,所以有![]() ;我們記“
;我們記“![]() ”即
”即![]() 時,方程
時,方程![]() 為倍根方程;
為倍根方程;
下面我們根據此結論來解決問題:
(1)方程①![]() ;方程②
;方程②![]() ;方程③
;方程③![]() 這幾個方程中,是倍根方程的是_________(填序號即可);
這幾個方程中,是倍根方程的是_________(填序號即可);
(2)若![]() 是倍根方程,則
是倍根方程,則![]() 的值為______;
的值為______;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線l1∥l2,直線l3和直線l1,l2交于C、D兩點,點P在直線CD上.
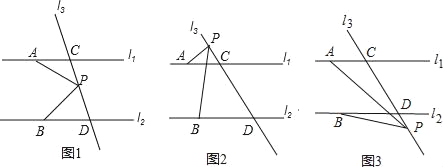
(1)試寫出圖1中∠APB、∠PAC、∠PBD之間的關系,并說明理由;
(2)如果P點在C、D之間運動時,∠APB、∠PAC、∠PBD之間的關系會發生變化嗎?
答: (填發生或不發生)
(3)若點P在C、D兩點的外側運動時(P點與點C、D不重合),如圖2,圖3,試分別寫出∠PAC、∠APB、∠PBD之間的關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】青島市某大酒店豪華間實行淡季、旺季兩種價格標準,旺季每間比淡季上漲![]() ,下表是去年該酒店豪華間某兩天的相關記錄:
,下表是去年該酒店豪華間某兩天的相關記錄:
旺季 | 淡季 | |
未入住房間數 | 10 | 0 |
日總收入(元) | 24 000 | 40 000 |
(1)該酒店豪華間有多少間?旺季每間價格為多少元
(2)今年旺季來臨,豪華間的間數不變。經市場調查發現,如果豪華間仍舊實行去年旺季價格,那么每天都客滿;如果價格繼續上漲,那么每增加25元,每天未入住房間數增加1間。不考慮其他因素,該酒店將豪華間的價格上漲多少元時,豪華間的日總收入最高?最高日總收入是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有下列四種結論:①AB=AD;②∠B=∠D;③∠BAC=∠DAC;④BC=DC.以其中的2個結論作為依據不能判定△ABC≌△ADC的是( )
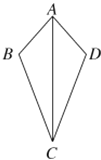
A. ①② B. ①③ C. ①④ D. ②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1個單位長度的小正方形組成的網格中,給出了格點△ABC(頂點是網格線的交點)和格點P.
(1)以A點為位似中心,將△ABC在網格中放大成△AB1C1,使![]() =2,請畫出△AB1C1;
=2,請畫出△AB1C1;
(2)以P點為三角形的一個頂點,請畫一個格點△PMN,使△PMN∽△ABC,且相似比為![]() .
.
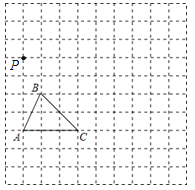
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com