
【題目】已知在平面直角坐標系中有三點![]() 、
、![]() 、
、![]() ,請回答如下問題:
,請回答如下問題:
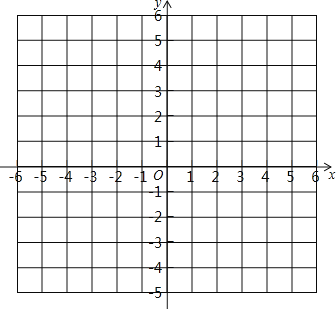
(1)在坐標系內描出點![]() 的位置:
的位置:
(2)求出以![]() 三點為頂點的三角形的面積;
三點為頂點的三角形的面積;
(3)在![]() 軸上是否存在點
軸上是否存在點![]() ,使以
,使以![]() 三點為頂點的三角形的面積為10,若存在,請直接寫出點
三點為頂點的三角形的面積為10,若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
科目:初中數學 來源: 題型:
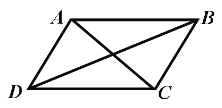
【題目】如圖,四邊形ABCD是平行四邊形,下列說法不正確的是( )
A. 當AC=BD時,四邊形ABCD是矩形
B. 當AB=BC時,四邊形ABCD是菱形
C. 當AC⊥BD時,四邊形ABCD是菱形
D. 當∠DAB=90°時,四邊形ABCD是正方形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下面的證明.
已知,如圖所示,BCE,AFE是直線,
AB∥CD,∠1=∠2,∠3=∠4.
求證:AD∥BE
證明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵∠1 =∠2 (已知)
∴∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有理數a,b,c在數軸上的位置如圖所示,且表示數a的點、數b的點與原點的距離相等.
![]()
(1)用“<”連接0,a, b, —1
(2)|b-1|+|a-1|=___
(3)化簡|a —b|+|a-c|-|b|+|b-c|
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
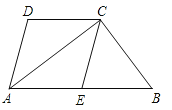
(1)求證:四邊形AECD是菱形;
(2)若點E是AB的中點,試判斷△ABC的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某車間為了改變管理松懈的狀況,準備采取每天任務定額和超產有獎的措施,從而提高工作效率.下面是該車間15名工人過去一天中各自裝配機器的數量(單位:臺):
15,6,16,7,15,8,7,13,8,11,8,10,9,10,9.
請回答下列問題:
(1)這組數據的平均數、眾數和中位數各是多少(結果精確到0.01臺)?
(2)管理者應確定每人標準日產量為多少臺比較合適?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新興服裝廠生產一種夾克和T恤,夾克每件定價![]() 元,T恤每件定價
元,T恤每件定價![]() 元.廠方在開展促銷活動期間,向客戶提供兩種優(yōu)惠方案:①買一件夾克送一件T恤;②夾克和T恤都按定價的
元.廠方在開展促銷活動期間,向客戶提供兩種優(yōu)惠方案:①買一件夾克送一件T恤;②夾克和T恤都按定價的![]() 付款.現某客戶要到該服裝廠購買夾克
付款.現某客戶要到該服裝廠購買夾克![]() 件,T恤
件,T恤![]() 件(
件(![]() ).
).
(1)若該客戶按方案①購買,夾克需付款________元,T恤需付款________元(用含![]() 的式子表示);若該客戶按方案②購買,夾克需付款______元,T恤需付款______元(用含
的式子表示);若該客戶按方案②購買,夾克需付款______元,T恤需付款______元(用含![]() 的式子表示);
的式子表示);
(2)若![]() ,通過計算說明按方案①、方案②哪種方案購買較為合算?
,通過計算說明按方案①、方案②哪種方案購買較為合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D是△ABC內一點,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H分別是AB,AC,CD,BD的中點,則四邊形EFGH的周長是( )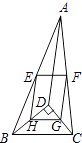
A.7
B.9
C.10
D.11
查看答案和解析>>
科目:初中數學 來源: 題型:
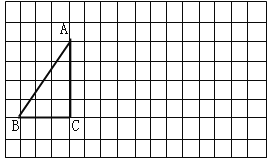
【題目】將下列方格紙中的△ABC向右平移7格,再向下平移2格,得到△![]() .(1)畫出平移后的三角形;
.(1)畫出平移后的三角形;
(2)若AB=5,則![]() = .
= .
(3)連接AA1,BB1, 根據“圖形平移”的性質,得:線段AA1與線段BB1的數量關系和位置關系是: .
(4)求圖中∠![]() AC+∠
AC+∠![]() BC的度數.
BC的度數.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com