
【題目】如圖,A(3,m)是反比例函數y=![]() 在第一象限圖象上一點,連接OA,過A作AB∥x軸,連接OB,交反比例函數y=
在第一象限圖象上一點,連接OA,過A作AB∥x軸,連接OB,交反比例函數y=![]() 的圖象于點P(2
的圖象于點P(2![]() ,
,![]() ).
).
(1)求m的值和點B的坐標;
(2)連接AP,求△OAP的面積.
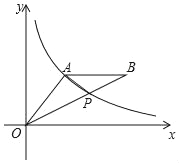
【答案】(1)m=4,點B的坐標為(8,4);(2)5![]() .
.
【解析】
(1)將點P的坐標代入解析式求解可得解析式,再把A點的坐標代入得到m的值,利用勾股定理求得AB=OA=5,由AB∥x軸即可得點B的坐標;
(2)根據點B坐標和點P的坐標,得到AE=1、PE=3![]() 、PD=
、PD=![]() ,再利用割補法求解可得.
,再利用割補法求解可得.
(1)將P(2![]() ,
,![]() )代入y═
)代入y═![]() ,得:k=12,
,得:k=12,
則反比例函數解析式為y=![]() ,
,
把A(3,m)代入y=![]() 得m=4,
得m=4,
如圖,過點A作AC⊥x軸于點C,
則OC=3、AC=4,
∴OA=![]() =5,
=5,
∵AB∥x軸,且AB=OA=5,
∴點B的坐標為(8,4);
(3)∵點B坐標為(8,4),
點P坐標為(2![]() ,
,![]() ),
),
過點P作PD⊥x軸,延長DP交AB于點E,
則點E坐標為(2![]() ,4),
,4),
∴AE=2![]() ﹣3、PE=4﹣
﹣3、PE=4﹣![]() 、PD=
、PD=![]() ,
,
則△OAP的面積=![]() ×(4+
×(4+![]() )×(2
)×(2![]() ﹣3)=5
﹣3)=5![]() .
.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:初中數學 來源: 題型:
【題目】某藥品研究所開發一種抗菌新藥,經多年動物實驗,首次用于臨床人體試驗,測得成人服藥后血液中藥物濃度y(微克/毫升)與服藥時間x小時之間函數關系如圖所示(當4≤x≤10時,y與x成反比例).
(1)根據圖象分別求出血液中藥物濃度上升和下降階段y與x之間的函數關系式.
(2)問血液中藥物濃度不低于2微克/毫升的持續時間多少小時?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,對角線AC=8,BD=6,點E,F分別是邊AB,BC的中點,點P在AC上運動,在運動過程中,存在PE+PF的最小值,則這個最小值是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,△ABC 頂點 A(2,3).若以原點 O 為位似中心,畫三角形 ABC
的位似圖形△A′B′C′,使△ABC 與△A′B′C′的相似比為![]() ,則 A′的坐標為( )
,則 A′的坐標為( )
A. (3,![]() ) B. (
) B. (![]() ,6) C. (3,
,6) C. (3,![]() )或(-3,-
)或(-3,-![]() ) D. (
) D. (![]() ,6)或(-
,6)或(-![]() ,-6)
,-6)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于反比例函數y=![]() (k≠0),下列所給的四個結論中,正確的是( )
(k≠0),下列所給的四個結論中,正確的是( )
A. 若點(2,4)在其圖象上,則(﹣2,4)也在其圖象上
B. 當k>0時,y隨x的增大而減小
C. 過圖象上任一點P作x軸、y軸的垂線,垂足分別A、B,則矩形OAPB的面積為k
D. 反比例函數的圖象關于直線y=x和y=﹣x成軸對稱
查看答案和解析>>
科目:初中數學 來源: 題型:
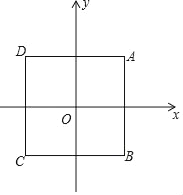
【題目】如圖,在平面直角坐標系xOy中,點O為正方形ABCD對角線的交點,且正方形ABCD的邊均與某條坐標軸平行或垂直,AB=4.
(1)如果反比例函數y=![]() 的圖象經過點A,求這個反比例函數的表達式;
的圖象經過點A,求這個反比例函數的表達式;
(2)如果反比例函數y=![]() 的圖象與正方形ABCD有公共點,請直接寫出k的取值范圍.
的圖象與正方形ABCD有公共點,請直接寫出k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線![]() 先向右平移2個單位,再向下平移2個單位,得到拋物線
先向右平移2個單位,再向下平移2個單位,得到拋物線![]() .
.

(1)求拋物線![]() 的解析式(化為一般式);
的解析式(化為一般式);
(2)直接寫出拋物線![]() 的對稱軸與兩段拋物線弧圍成的陰影部分的面積.
的對稱軸與兩段拋物線弧圍成的陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 為
為![]() 的切線,
的切線,![]() 為切點,直線
為切點,直線![]() 交
交![]() 于點
于點![]() 、
、![]() ,過點
,過點![]() 作
作![]() 的垂線
的垂線![]() ,垂足為點
,垂足為點![]() ,交
,交![]() 于點
于點![]() ,延長
,延長![]() 與
與![]() 交于點
交于點![]() ,連接
,連接![]() ,
,![]() .
.
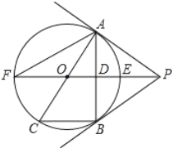
(1)求證:直線![]() 為
為![]() 的切線;
的切線;
(2)試探究線段![]() 、
、![]() 、
、![]() 之間的等量關系,并加以證明;
之間的等量關系,并加以證明;
(3)若![]() ,
,![]() ,求
,求![]() 的值和線段
的值和線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是小強洗漱時的側面示意圖,洗漱臺(矩形ABCD)靠墻擺放,高AD=80cm,寬AB=48cm,小強身高166cm,下半身FG=100cm,洗漱時下半身與地面成80°(∠FGK=80°),身體前傾成125°(∠EFG=125°),腳與洗漱臺距離GC=15cm(點D,C,G,K在同一直線上).
(1)此時小強頭部E點與地面DK相距多少?
(2)小強希望他的頭部E恰好在洗漱盆AB的中點O的正上方,他應向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,結果精確到0.1cm)
≈1.41,結果精確到0.1cm)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com