
 ,﹣3)或(1﹣
,﹣3)或(1﹣ ,﹣3)
,﹣3) ,
, )
)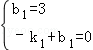 ,解得
,解得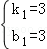 ,
,
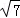 ,﹣3);
,﹣3);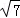 ,﹣3);
,﹣3);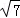 ,﹣3)或(1﹣
,﹣3)或(1﹣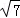 ,﹣3).
,﹣3).
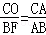 ,
,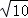 ,AB=4.
,AB=4.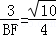 ,∴BF=
,∴BF=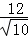 ,∴BB′=2BF=
,∴BB′=2BF=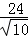 ,
,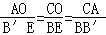 ,∴
,∴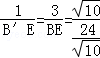 ,
,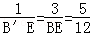 .∴B′E=
.∴B′E=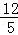 ,BE=
,BE=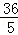 ,∴OE=BE﹣OB=
,∴OE=BE﹣OB=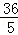 ﹣3=
﹣3=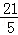 .
.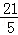 ,
,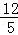 ).
).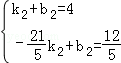 ,
, ,∴直線B'D的解析式為:y=
,∴直線B'D的解析式為:y=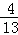 x+
x+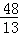 ,
,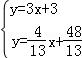 ,解得
,解得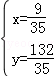 ,
, ,
,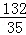 ).
).

科目:初中數學 來源:不詳 題型:解答題
 x+150,成本為40元/件,無論銷售多少,每月還需支出房租費52500元,設月利潤為w專(元)(利潤 = 銷售額-成本-廣告費).若只是電視直銷,銷售價格為150元/件,受各種不確定因素影響,成本為a元/件(a為常數,40≤a≤80),當月銷量為x(件)時,每月還需繳納
x+150,成本為40元/件,無論銷售多少,每月還需支出房租費52500元,設月利潤為w專(元)(利潤 = 銷售額-成本-廣告費).若只是電視直銷,銷售價格為150元/件,受各種不確定因素影響,成本為a元/件(a為常數,40≤a≤80),當月銷量為x(件)時,每月還需繳納 x2 元的廣告費,設月利潤為w電(元)(利潤 = 銷售額-成本-附加費).
x2 元的廣告費,設月利潤為w電(元)(利潤 = 銷售額-成本-附加費).查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 x2+3x+1的一部分,
x2+3x+1的一部分, (2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳點A的水平距離是4米,問這表是
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳點A的水平距離是4米,問這表是查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 ,0)和點B,將拋物線沿x軸向上翻折,頂點P落在點P'(1,3)處.
,0)和點B,將拋物線沿x軸向上翻折,頂點P落在點P'(1,3)處.
 .請你計算這個“W”圖案的高與寬的比到底是多少?
.請你計算這個“W”圖案的高與寬的比到底是多少?查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
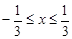 時有最大值-4,求a的值.(5分)
時有最大值-4,求a的值.(5分)查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
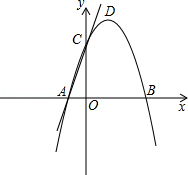
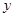 軸的負半軸于點C,則點C的坐標為 ,若二次函數
軸的負半軸于點C,則點C的坐標為 ,若二次函數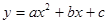 的圖像經過點A,C,B.已知點P是該拋物線上的動點,當∠APB是銳角時,點P的橫坐標
的圖像經過點A,C,B.已知點P是該拋物線上的動點,當∠APB是銳角時,點P的橫坐標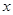 的取值范圍是 .
的取值范圍是 .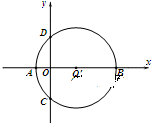
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com