產品按質量可分成6種不同的檔次,若工時不變,每天可生產最低檔次的產品40件,如果每提高一個檔次,每件利潤可增加1元,但每天要少生產2件產品.
(1)若最低檔次的產品每件利潤為16元時,生產哪種檔次的產品所得利潤最大?
(2)若最低檔次的產品每件利潤為22元時,生產哪種檔次的產品所得利潤最大?
(3)由于原材料價格浮動,生產最低檔次的產品每件利潤可以從8元到24元不等,那么生產哪種檔次的產品所得利潤最大?
解:(1)設生產第x檔次的產品,獲得利潤為y元,則y=[40-2(x-1)][16+(x-1)],
y=-2(x-3)
2+648
故當x=3時獲得的最大利潤為648元.
(2)設生產第n檔次的產品,獲得利潤為m元,則m=[40-2(n-1)][22+(n-1)],
m=-2n
2+882.
∵a=-2<0,對稱軸為y軸.
∴拋物線開口下向下,在對稱軸的右側m隨n的增大而減小.
∴當n=1時,m最大為880元.
(3)設生產最低檔次的產品每件利潤為a元,生產第x檔次的產品,獲得利潤為y元,
則y=[40-2(x-1)][a+(x-1)]
y=-2(x-
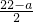
)
2+
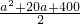
,
則當x=
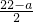
時,y
最大=
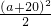
,
∵8≤a≤24,x為1~6的整數,
∴
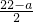
>0,a取最大值時,y最大,
∴a<22,
∴要使y最大,必須a=20,x=
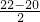
=1.
即生產第1檔次的產品所得利潤最大.
分析:(1)關系式為:利潤=(最低檔次的利潤+檔次-1)×[原來可生產產品件數-2(檔次-1)],求得相關代數式后,可利用頂點式求得相應的對稱軸,進而根據檔次為整數求得離對稱軸最近的整數檔次即可;
(2)結合(1)可得相應關系式,進而用頂點式可得相應的最大值,根據生產最低檔次的產品每件利潤的取值范圍可得相應檔次產品的檔次.
(3)結合(1)可得相應關系式,進而用頂點式可得相應的最大值,根據生產最低檔次的產品每件利潤的取值范圍可得相應檔次產品的檔次.
點評:本題考查二次函數的應用;得到每件產品的利潤及銷售量是解決本題的關鍵;根據最低檔次的產品的利潤的相應的取值判斷出相應檔次是解決本題的難點.

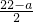 )2+
)2+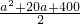 ,
,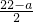 時,y最大=
時,y最大=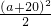 ,
,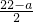 >0,a取最大值時,y最大,
>0,a取最大值時,y最大,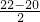 =1.
=1.

 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案