【題目】“校園安全”受到全社會的廣泛關注，某校政教處對部分學生及家長就校園安全知識的了解程度進行了隨機抽樣調查，并繪制成如圖所示的兩幅統計圖，請根據統計圖中的信息，解答下列問題:
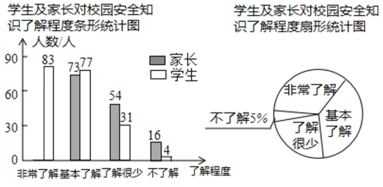
參與調查的學生及家長共有 人；
在扇形統計圖中，求“基本了解"所對應的扇形的圓心角的度數；
在條形統計圖中，“非常了解”所對應的學生人數是______人 并補全條形統計圖．
名校名師培優作業本加核心試卷系列答案
全程金卷系列答案科目：初中數學 來源： 題型：
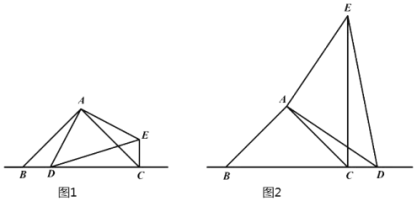
【題目】已知:△ABC和△ADE均為等腰直角三角形，∠BAC=∠DAE=90°，點D是等腰直角三角形ABC斜邊BC所在直線上一點(不與點B重合).
(1)如圖1，當點D在線段BC上時，線段CE、BD之間的位置關系是__________，數量關系是___________；
(2)如圖2，當點D在線段BC的延長線上時，探索AD、BD、CD三條線段之間的數量關系，寫出結論并證明；
(3)若BD=
CD，直接寫出∠BAD的度數。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料:我們知道a的幾何意義是在數軸上數a對應的點與原點的距離.數軸上數a與數0對應點之間的距離，
這 個結論可以推廣為: |a- b|均表示在數軸上數a與b對應點之間的距離，例:已知|a-1|=2， 求a的值.
解:在數軸上與1的距離為2點的對應數為3和-1，即a的值為3和-1.
仿照閱讀材料的解法，解決下列問題
(1)已知
，求a的值.
(2)若數軸上表示a的點在-4與2之間，則|a+4|+|a-2|的值為___
(3)當a滿足什么條件時，|a-1|+ |a+2|有最小值，最小值是多少?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀第①小題的計算方法，再計算第②小題．
①–5
+（–9
）+17
+（–3
）
解：原式=[（–5）+（–）]+[（–9）+（–）]+（17+）+[（–3+（–）]
=[（–5）+（–9）+（–3）+17]+[（–）+（–）+（–）+]
=0+（–1
）
=–1．
上述這種方法叫做拆項法．靈活運用加法的交換律、結合律可使運算簡便．
②仿照上面的方法計算：（﹣2000）+（﹣1999）+4000+（﹣1）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】考試前夕，為“連粽連中”的吉祥寓意，某校食堂購進甲、乙兩種粽子520個，其中甲種粽子花費600元，乙種粽子花費800元，已知甲種粽子單價比乙種粽子單價高20%，乙種粽子的單價是多少元？甲、乙兩種粽子各購買了多少個？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，平面直角坐標系中，矩形OABC的頂點A（6，0）、B（6，4），D是BC的中點．動點P從O點出發，以每秒1個單位的速度，沿著OA、AB、BD運動．設P點運動的時間為t秒（0<t<13）．
（1）寫出△POD的面積S與t之間的函數關系式，并求出△POD的面積等于9時點P的坐標；
（2）當點P在OA上運動時，連結CP．問：是否存在某一時刻t，當CP繞點P旋轉時，點C能恰好落到AB的中點M處？若存在，請求出t的值并判斷此時△CPM的形狀；若不存在，請說明理由；
（3）當點P在AB上運動時，試探索當PO+PD的長最短時的直線PD的表達式。
查看答案和解析>>
科目：初中數學 來源： 題型：
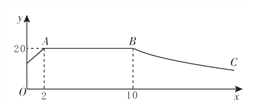
【題目】我市某蔬菜生產基地在氣溫較低時，用裝有恒溫系統的大棚栽培一種在自然光照且大棚內溫度為20℃的條件下生長最快的新品種．如圖是某天恒溫系統從開啟到關閉后大棚內溫度y（單位：℃）隨光照時間x（單位：h）變化的大致圖象，其中BC段是雙曲線
的一部分．請根據圖中信息解答下列問題：
（1）這天恒溫系統在保持大棚內溫度20℃的時間有 h；
（2）求k的值；
（3）當x=16 h時，大棚內的溫度約為多少℃？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形OABC的頂點A，C分別在ｘ軸和ｙ軸上，點B的坐標為（2，3）。雙曲線
的圖像經過BC的中點D，且與AB交于點E，連接DE。
（1）求k的值及點E的坐標；
（2）若點F是邊上一點，且△FBC∽△DEB，求直線FB的解析式
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
