
【題目】如圖,正方形ABCD的邊長為2,E、F分別為BC,CD的中點,連接AE,BF交于點G,將△BCF沿BF對折,得到△BPF,延長FP交AD于點M,交BA的延長線于點Q.連接BM,下列結論中:①AE=BF; ②AE⊥BF;③AQ=![]() ;④∠MBF=60°.
;④∠MBF=60°.
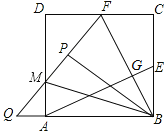
正確的結論是_____(填正確結論的序號).
【答案】①②③
【解析】
由題意可證△BFC≌△ABE,可判斷①②,由折疊可判斷④,根據勾股定理可求AM=![]() ,DM=
,DM=![]() ,根據平行線分線段成比例可求AQ=
,根據平行線分線段成比例可求AQ=![]() ,可判斷③
,可判斷③
∵四邊形ABCD是正方形,
∴AB=BC=AD=CD=2,∠C=∠D=∠ABC=90°,
∵CF=BE,AB=BC,∠C=∠ABC,
∴△AEB≌△BCF,
∴AE=BF,∠EAB=∠FBC,
∵∠FBC+∠ABF=90°,
∴∠EAB+∠ABF=90°,
∴∠AGB=90°即AE⊥BF,
故①②正確,
∵折疊,
∴BC=BP,∠CBF=∠PBF,
∴AB=BP且BM=BM,
∴Rt△ABM≌Rt△BMP,
∴AM=MP,∠ABM=∠PBM,
∵∠ABM+∠PBM+∠CBF+∠PBF=90°,
∴∠MBF=45°,
故④錯誤,
∵在Rt△DMF中,MF2=FD2+DM2.
∴(1+AM)2=(2-AM)2+1,
∴AM=![]() ,
,
∴DM=![]() ,
,
∵CD∥BA,
∴![]() ,
,
∴AQ=![]()
故③正確
故答案是:①②③


科目:初中數學 來源: 題型:
【題目】如圖,已知⊙O是△ABC的外接圓,連接OC,過點A作AD∥OC,交BC的延長線于D,AB交OC于E,∠ABC=45°.
(1)求證:AD是⊙O的切線;
(2)若AE=![]() ,CE=3.
,CE=3.
①求⊙O的半徑;
②求圖中陰影部分的面積.
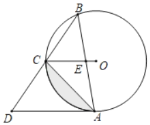
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖,則下列結論錯誤的是( )
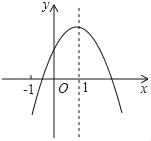
A. 4a+2b+c>0B. abc<0C. b<a﹣cD. 3b>2c
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知拋物線y=﹣x2+bx+c與x軸相交于A、B兩點,且點A的坐標為(1,0),與y軸交于點C,對稱軸直線x=2與x軸相交于點D,點P是拋物線對稱軸上的一個動點,以每秒1個單位長度的速度從拋物線的頂點E向下運動,設點P運動的時間為t(s).
(1)點B的坐標為 ,拋物線的解析式是 ;
(2)求當t為何值時,△PAC的周長最小?
(3)當t為何值時,△PAC是以AC為腰的等腰三角形?
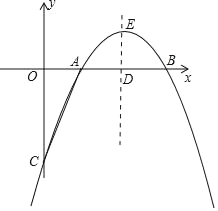
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題提出:
有n個環環相扣的圓環形成一串線型鏈條,當只斷開其中的k(k<n)個環,要求第一次取走一個環,以后每次都只能比前一次多得一個環,則最多能得到的環數n是多少呢?
問題探究:
為了找出n與k之間的關系,我們運用一般問題特殊化的方法,從特殊到一般,歸納出解決問題的方法.
探究一:k=1,即斷開鏈條其中的1個環,最多能得到幾個環呢?
當n=1,2,3時,斷開任何一個環,都能滿足要求,分次取走;
當n=4時,斷開第二個環,如圖①,第一次取走1環;第二次退回1環換取2環,得2個環;第三次再取回1環,得3個環;第四次再取另1環,得4個環,按要求分4次取走.
當n=5,6,7時,如圖②,圖③,圖④方式斷開,可以用類似上面的方法,按要求分5,6,7次取走.
當n=8時,如圖⑤,無論斷開哪個環,都不可能按要求分次取走.
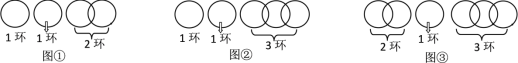
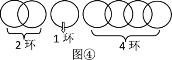
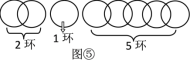
所以,當斷開1個環時,從得到更多環數的角度考慮,把鏈條分成3部分,分別是1環、2環和4環,最多能得到7個環.
即當k=1時,最多能得到的環數n=1+2+4=1+2×3=1+2×(22-1)=7.
探究二:k=2,即斷開鏈條其中的2個環,最多能得到幾個環呢?
從得到更多環數的角度考慮,按圖⑥方式斷開,把鏈條分成5部分,按照類似探究一的方法,按要求分1,2,…23次取走.
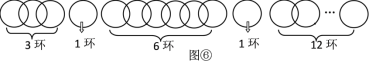
所以,當斷開2個環時,把鏈條分成5部分,分別是1環、1環、3環、6環、12環,最多能得到23個環.
即當k=2時,最多能得到的環數n=1+1+3+6+12=2+3×7=2+3×(23-1)=23.
探究三:k=3,即斷開鏈條其中的3個環,最多能得到幾個環呢?
從得到更多環數的角度考慮,按圖⑦方式斷開,把鏈條分成7部分,按照類似前面探究的方法,按要求分1,2,…63次取走.
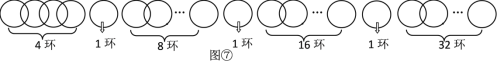
所以,當斷開3個環時,從得到更多環數的角度考慮,把鏈條分成7部分,分別是1環、1環、1環、4環、8環、16環、32環,最多能得到63個環.
即當k=3時,最多能得到的環數n=1+1+1+4+8+16+32=3+4×15=3+4×(24-1)=63.
探究四:k=4,即斷開鏈條其中的4個環,最多能得到幾個環呢?
按照類似前面探究的方法,當斷開4個環時,從得到更多環數的角度考慮,把鏈條分成 部分,分別為 ,最多能得到的環數n= .請畫出如圖⑥的示意圖.
模型建立:
有n個環環相扣的圓環形成一串線型鏈條,斷開其中的k(k<n)個環,從得到更多環數的角度考慮,把鏈條分成 部分,
分別是:1、1、1……1、k+1、 、……、 ,最多能得到的環數n = .
實際應用:
一天一位財主對雇工說:“你給我做兩年的工,我每天付給你一個銀環.不過,我用一串環環相扣的線型銀鏈付你工錢,但你最多只能斷開銀鏈中的6個環.如果你無法做到每天取走一個環,那么你就得不到這兩年的工錢,如果銀鏈還有剩余,全部歸你!你愿意嗎?”
聰明的你是否可以運用本題的方法通過計算幫助雇工解決這個難題,雇工最多能得到總環數為多少環的銀鏈?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知y關于x二次函數y=x2﹣(2k+1)x+(k2+5k+9)與x軸有交點.
(1)求k的取值范圍;
(2)若x1,x2是關于x的方程x2﹣(2k+1)x+(k2+5k+9)=0的兩個實數根,且x12+x22=39,求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,正方形ABCD的頂點A的坐標為(﹣1,1),點B在x軸正半軸上,點D在第三象限的雙曲線y=![]() 上,過點C作CE∥x軸交雙曲線于點E,連接BE,則△BCE的面積為( )
上,過點C作CE∥x軸交雙曲線于點E,連接BE,則△BCE的面積為( )
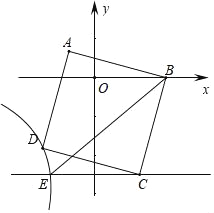
A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=8,AD=3.點E從D向C以每秒1個單位的速度運動,以AE為一邊在AE的右下方作正方形AEFG.同時垂直于CD的直線MN也從C向D以每秒2個單位的速度運動,當經過多少秒時.直線MN和正方形AEFG開始有公共點?( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com